In this chapter I will provide a variety of background material that will be used in later chapters. Later chapters will include links to the relevant sections of this chapter. I cover a variety of topics:

• Section 2.1 gives an overview of how proof assistants are designed. This provides some context to place this thesis within the field of ITP.

• Section 2.2 contains some preliminary definitions and notation for types, terms, datatypes and functors that will be used throughout the document.

• Section 2.3 contains some additional features of inductive datatypes that I will make use of in various places throughout the text.

• Section 2.4 discusses the way in which metavariables and tactics work within the Lean theorem prover, the system in which the software I write is implemented.

• Section 2.5 asks what it means for a person to understand or be confident in a proof. This is used to motivate the work in Chapter 3 and Chapter 4. It is also used to frame the user study I present in Chapter 6.

• Section 2.6 explores what the automated reasoning literature has to say on how to define and make use of 'human-like reasoning'. This includes a survey of proof planning (Section 2.6.2).

• Section 2.7 surveys the topic of natural language generation of mathematical texts, used in Section 3.6.

2.1. The architecture of proof assistants

In this section I am going to provide an overview of the designs of proof assistants for non-specialist. The viewpoint I present here is largely influenced by the viewpoint that Andrej Bauer expresses in a MathOverflow answer [Bau20[Bau20]Bauer, AndrejWhat makes dependent type theory more suitable than set theory for proof assistants? (2020)https://mathoverflow.net/q/376973].

The essential purpose of a proof assistant is to represent mathematical theorems, definitions and proofs in a language that can be robustly checked by a computer. This language is called the foundation language equipped with a set of derivation rules. The language defines the set of objects that formally represent mathematical statements and proofs, and the inference rules and axioms provide the valid ways in which these objects can be manipulatedAt this point, we may raise a number of philosophical objections such as whether the structures and derivations 'really' represent mathematical reasoning. The reader may enjoy the account given in the first chapter of Logic for Mathematicians by J. Barkley Rosser [Ros53].. Some examples of foundations are first-order logic (FOL), higher-order logic (HOL), and various forms of dependent type theory (DTT) [Mar84, CH88, PP89, Pro13].

A component of the software called the kernel checks proofs in the foundation. There are numerous foundations and kernel designs. Finding new foundations for mathematics is an open research area but FOL, HOL and DTT mentioned above are the most well-established for performing mathematics. I will categorise kernels as being either 'checkers' or 'builders'.

A 'checker' kernel takes as input a proof expression and outputs a yes/no answer to whether the term is a valid proof. An example of this is the Lean 3 kernel [MKA+15[MKA+15]de Moura, Leonardo; Kong, Soonho; Avigad, Jeremy; et al.The Lean theorem prover (system description) (2015)International Conference on Automated Deductionhttps://doi.org/10.1007/978-3-319-21401-6_26].

A 'builder' kernel provides a fixed set of partial functions that can be used to build proofs. Anything that this set of functions accepts is considered as valid. This is called an LCF architecture, originated by Milner [Mil72[Mil72]Milner, RobinLogic for computable functions description of a machine implementation (1972)Technical Reporthttps://apps.dtic.mil/dtic/tr/fulltext/u2/785072.pdf, Gor00[Gor00]Gordon, MikeFrom LCF to HOL: a short history (2000)Proof, language, and interactionhttp://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.132.8662&rep=rep1&type=pdf]. The most widely used 'builder' is the Isabelle kernel by Paulson [Pau89[Pau89]Paulson, Lawrence CThe foundation of a generic theorem prover (1989)Journal of Automated Reasoninghttps://doi.org/10.1007/BF00248324].

Most kernels stick to a single foundation or family of foundations. The exception is Isabelle, which instead provides a 'meta-foundation' for defining foundations, however the majority of work in Isabelle uses the HOL foundation.

2.1.1. The need for a vernacular

One typically wants the kernel to be as simple as possible, because any bugs in the kernel may result in 'proving' a false statement An alternative approach is to 'bootstrap' increasingly complex kernels from simpler ones. An example of this is the Milawa theorem prover for ACL2 [Dav09].. For the same reason, the foundation language should also be as simple as possible. However, there is a trade-off between kernel simplicity and the usability and readability of the foundation language; a simplified foundation language will lack many convenient language features such as implicit arguments and pattern matching, and as a result will be more verbose. If the machine-verified definitions and lemmas are tedious to read and write, then the prover will not be adopted by users.

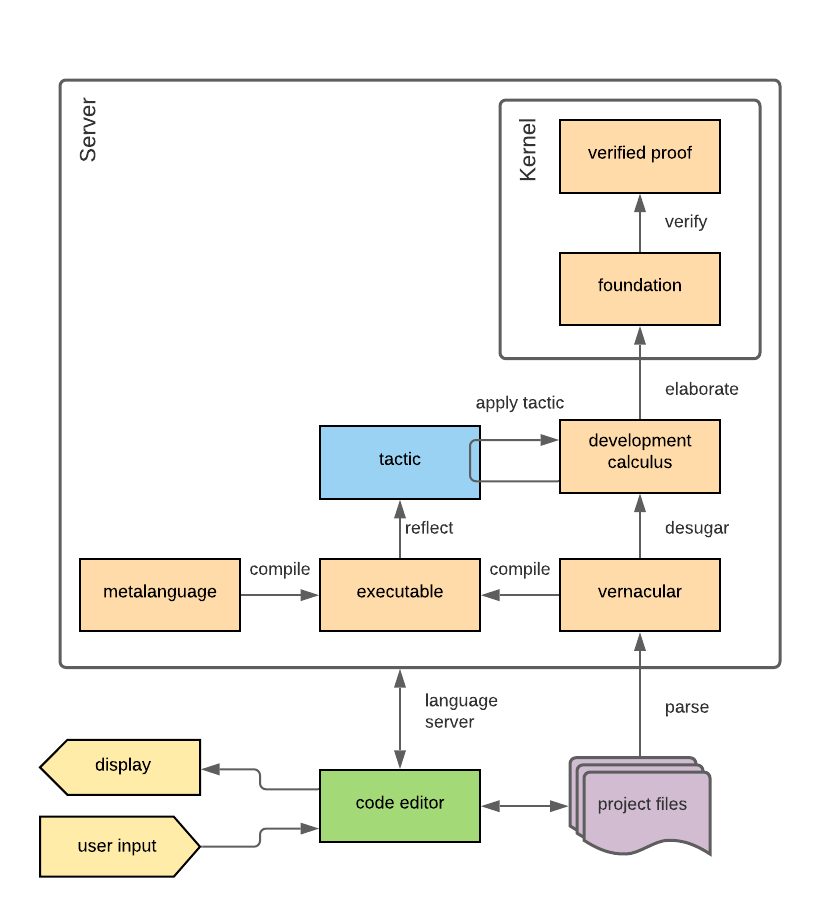
Proof assistant designers need to bridge this gap between a human-readable, human-understandable proof and a machine-readable, machine-checkable proof. A common approach is to use a second language called the vernacular (shown on Figure 2.5). The vernacular is designed as a human-and-machine-readable compromise that is converted to the foundation language through a process called elaboration (e.g., [MAKR15[MAKR15]de Moura, Leonardo; Avigad, Jeremy; Kong, Soonho; et al.Elaboration in Dependent Type Theory (2015)CoRRhttp://arxiv.org/abs/1505.04324]). The vernacular typically includes a variety of essential features such as implicit arguments and some form of type inference, as well as high-level programming features such as pattern matching. Optionally, there may be a compiler (see Figure 2.5) for the vernacular to also produce runnable code, for example Lean 3 can compile vernacular to bytecode [EUR+17[EUR+17]Ebner, Gabriel; Ullrich, Sebastian; Roesch, Jared; et al.A metaprogramming framework for formal verification (2017)Proceedings of the ACM on Programming Languageshttps://doi.org/10.1145/3110278].

I discuss some work on provers with the vernacular being a restricted form of natural language as one might find in a textbook in Section 2.7.2.

2.1.2. Programs for proving

Using a kernel for checking proofs and a vernacular structure for expressing theorems, we now need to be able to construct proofs of these theorems.

An Automated Theorem Prover (ATP) is a piece of software that produces proofs for a formal theorem statement automatically with a minimal amount of user input as to how to solve the proof, examples include Z3, E and Vampire.

Interactive Theorem Proving (ITP) is the process of creating proofs incrementally through user interaction with a prover. I will provide a review of user interfaces for ITP in Section 5.1. Most proof assistants incorporate various automated and interactive theorem proving components. Examples of ITPs include Isabelle [Pau89], Coq [Coq], Lean [MKA+15], HOL Light [Har09], Agda [Nor08], Mizar [GKN15], PVS [SORS01].

A common modality for allowing the user to interactively construct proofs is with the proof script (Figure 2.1), this is a sequence of textual commands, written by the user to invoke certain proving programs called tactics that manipulate a state representing a partially constructed proof. An example of a tactic is the assume tactic in Figure 2.1, which converts a goal-state of the form ⊢ X → Y to X ⊢ Y. Some of these tactics my invoke various ATPs to assist in constructing proofs. Proof scripts may be purely linear as in Figure 2.1 or have a hierarchical structure such as in Isar [Wen99[Wen99]Wenzel, MarkusIsar - A Generic Interpretative Approach to Readable Formal Proof Documents (1999)Theorem Proving in Higher Order Logicshttps://doi.org/10.1007/3-540-48256-3_12] or HiProof [ADL10[ADL10]Aspinall, David; Denney, Ewen; Lüth, ChristophTactics for hierarchical proof (2010)Mathematics in Computer Sciencehttps://doi.org/10.1007/s11786-010-0025-6].

An alternative to a proof script is for the prover to generate an auxiliary proof object file that holds a representation of the proof that is not intended to be human readable. This is the approach taken by PVS [SORS01[SORS01]Shankar, Natarajan; Owre, Sam; Rushby, John M; et al.PVS prover guide (2001)Computer Science Laboratory, SRI International, Menlo Park, CAhttps://pvs.csl.sri.com/doc/pvs-prover-guide.pdf] although I will not investigate this approach further in this thesis because most of the ITP systems use the proof-script approach.

In the process of proving a statement, a prover must keep track of partially built proofs. I will refer to these representations of partially built proofs as development calculi. I will return to development calculi in Section 2.4.

2.1.3. Foundation

A foundation for a prover is built from the following pieces:

1. A language: defining inductive trees of data that we wish to talk about and also syntax for these trees.

2. The judgements: meta-level predicates over the above trees.

3. The inference rules: a generative set of rules for deriving judgements from other judgements.

To illustrate, the language of simply typed lambda calculus would be expressed as in (2.2).

𝑥, 𝑦, 𝑧 ::= X                       -- variable
α, β    ::= A | α → β              -- type
𝑠, 𝑡    ::= 𝑠 𝑡 | λ (𝑥 : α), 𝑠 | X  -- term
Γ       ::= ∅ | Γ, (𝑥 : α)          -- context

In (2.2), the purple greek and italicised letters (𝑥, 𝑦, α, ...) are called nonterminals. They say: "You can replace me with any of the |-separated items on the right-hand-side of my ::=". So, for example, "α" can be replaced with either a member of A or "α → β". The green words in the final column give a natural language noun to describe the 'kind' of the syntax.

In general terms, contexts Γ perform the role of tracking which variables are currently in scope. To see why contexts are needed, consider the expression 𝑥 + 𝑦; its resulting type depends on the types of the variables 𝑥 and 𝑦. If 𝑥 and 𝑦 are both natural numbers, 𝑥 + 𝑦 will be a natural number, but if 𝑥 and 𝑦 have different types (e.g, vectors, strings, complex numbers) then 𝑥 + 𝑦 will have a different type too. The correct interpretation of 𝑥 + 𝑦 depends on the context of the expression.

Next, define the judgements for our system in (2.3). Judgements are statements about the language.

Then define the natural deduction rules (2.4) for inductively deriving these judgements.

And from this point, it is possible to start exploring the theoretical properties of the system. For example: is Γ ⊢ 𝑠 : α decidable?

Foundations such as the example above are usually written down in papers as a BNF grammar and a spread of gammas, turnstiles and lines as illustrated in (2.2), (2.3) and (2.4). LISP pioneer Steele calls it Computer Science Metanotation [Ste17[Ste17]Steele Jr., Guy L.It's Time for a New Old Language (2017)http://2017.clojure-conj.org/guy-steele/].

In implementations of proof assistants, the foundation typically doesn't separate quite as cleanly in to the above pieces. The language is implemented with a number of optimisations such as de Bruijn indexing [deB72[deB72]de Bruijn, Nicolaas GovertLambda calculus notation with nameless dummies, a tool for automatic formula manipulation, with application to the Church-Rosser theorem (1972)Indagationes Mathematicae (Proceedings)http://alexandria.tue.nl/repository/freearticles/597619.pdf] for the sake of efficiency. Judgements and rules are implicitly encoded in algorithms such as type checking, or appear in forms different from that in the corresponding paper. This is primarily for efficiency and extensibility.

In this thesis the formalisation language that I focus on is the calculus of inductive constructions (CIC) Calculus of Inductive Constructions. Inductive datastructures (Section 2.2.3) for the Calculus of Constructions [CH88] were first introduced by Pfenning et al [PP89]. This is the the type theory used by Lean 3 as implemented by de Moura et al and formally documented by Carneiro [Car19[Car19]Carneiro, MarioLean's Type Theory (2019)Masters' thesis (Carnegie Mellon University)https://github.com/digama0/lean-type-theory/releases/download/v1.0/main.pdf]. A good introduction to mathematical formalisation with dependent type theory is the first chapter of the HoTT Book [Pro13[Pro13]The Univalent Foundations ProgramHomotopy Type Theory: Univalent Foundations of Mathematics (2013)publisher Institute for Advanced Studyhttps://homotopytypetheory.org/book/ ch. 1]. Other foundations are also available: Isabelle's foundation is two-tiered [Pau89[Pau89]Paulson, Lawrence CThe foundation of a generic theorem prover (1989)Journal of Automated Reasoninghttps://doi.org/10.1007/BF00248324]: there is a meta-level foundation upon which many foundations can be implemented. A lot of the work in this thesis is independent of foundation and so I will try to indicate how the contributions can be augmented to work in other foundations.

A typical architecture of a modern, full-fledged checker-style proof assistant is given in Figure 2.5.

2.2. Preliminaries

This section contains a set of quick preliminary definitions for the concepts and notation that I will be using later. In this thesis I will be using a pseudo-language which should be familiar to functional programming enthusiasts. This pseudo-language is purely presentational and is used to represent algorithms and datastructures for working with theorem provers.

2.2.1. Some notation for talking about type theory and algorithms

The world is built of types and terms. New variables are introduced as "𝑥 : A"; 𝑥 is the variable and it has the type A. Lots of variables with the same type can be introduced as 𝑥 𝑦 𝑧 : A. Types A B C : Type start with an uppercase letter and are coloured turquoise. Type is a special 'type of types'. Meanwhile terms start with a lowercase letter and term variables are purple and italicised. A → B is the function type. → is right associative which means that 𝑓 : A → B → C should be read as 𝑓 : A → (B → C). This is called a curried function, we may consider A and B to be the input arguments of 𝑓 and C to be its return type. Given 𝑎 : A we may apply 𝑓 to 𝑎 by writing 𝑓 𝑎 : B → C. Functions are introduced using maps-to notation (𝑎 : A) ↦ (𝑏 : B) ↦ 𝑓 𝑎 𝑏. Write the identity function 𝑥 ↦ 𝑥 as 𝟙 : X → X. Given 𝑓 : A → B, 𝑔 : B → C, write function composition as 𝑔 ∘ 𝑓 : A → C. Function application is left associative, so 𝑓 𝑎 𝑏 should be read as (𝑓(𝑎))(𝑏). The input types of functions may optionally be given argument names, such as: (𝑎 : A) → (𝑏 : B) → C. We also allow 'dependent types' where the return value C is allowed to depend on these arguments: (𝑎 : A) → 𝒞 𝑎 where 𝒞 : A → Type is a type-valued function.

• Empty is the empty type.

• Unit is the type containing a single element ().

• Bool is the boolean type ranging over values true and false.

• Option X is the type taking values some 𝑥 for 𝑥 : X or none. some will usually be suppressed. That is, 𝑥 : X will be implicitly cast to some 𝑥 : Option X in the name of brevity.

• List X is the type of finite lists of X. Given 𝑥 𝑦 : X and 𝑙₁ 𝑙₂ : List X, we can write 𝑥 :: 𝑙₁ for list cons and 𝑙₁ ++ 𝑙₂ for concatenating (i.e, appending) two lists. For list construction and pattern matching, list spreads will be used. For example[..𝑙₁, 𝑥, 𝑦, ..𝑙₂] denotes the list formed by concatenating 𝑙₁, [𝑥, 𝑦] and 𝑙₂. Python-style list comprehensions are also used: [𝑖² for 𝑖 in 1..20] is a list of the first 20 square numbers.

• ℕ is the type of natural numbers. Individual numbers can be used as types: 𝑥 : 3 means that 𝑥 is a natural number taking any value 𝑥 < 3, i.e, 𝑥 ∈ {0,1,2}.

• A × B is the type of tuples over A and B. Elements are written as (a, b) : A × B. As usual we have projections π₁ (𝑎, 𝑏) := 𝑎 and π₂ (𝑎, 𝑏) := 𝑏. Members of tuples may be given names as (a : A) × (b : B). In this case, supposing p : (a : A) × (b : B), we can write p.a and p.b instead of π₁ p and π₂ p. Similarly to above, we can have a dependent tuple or 'sigma type' (a : A) × (b : B(a)).

• A + B is the discriminated union of A and B with constructors inl : A → A + B and inr : B → A + B.

2.2.2. Functors and monads

I will assume that the readers are already familiar with the motivation behind functors and monads in category theory and as used in e.g. Haskell but I will summarise them here for completeness. I refer the unfamiliar reader to the Haskell Typeclassopediahttps://wiki.haskell.org/Typeclassopedia.

Definition 2.6 (functor): A functor is a type-valued function F : Type → Type equipped with a function mapper F (𝑓 : A → B) : F A → F BHere, the word 'functor' is used to mean the special case of category-theoretical functors with the domain and codomain category being the category of Type.. I always assume that the functor is lawful, which here means it obeys the functor laws (2.7).

Definition 2.8 (natural function): A natural function a : F ⇒ G between functors F G : Type → Type is a family of functions a[A] : F A → G A indexed by A : Type such that a[B] ∘ F f = G f ∘ a[A] for all f : A → B. Often the type argument to a will be suppressed. It is quick to verify that the functors and natural functors over them form a category.

Definition 2.9 (monad): A monadFor learning about programming with monads, see https://wiki.haskell.org/All_About_Monads M : Type → Type is a functor equipped with two natural functions pure : 𝟙 ⇒ M and join : M M ⇒ M obeying the monad laws (2.10). Write 𝑚 >>= 𝑓 := join (M 𝑓 𝑚) for 𝑚 : M A and 𝑓 : A → M B. do notation is used in placeshttps://wiki.haskell.org/Keywords#do.

Definition 2.11 (applicative): An applicative functor [MP08[MP08]McBride, Conor; Paterson, RossApplicative programming with effects (2008)J. Funct. Program.https://personal.cis.strath.ac.uk/conor.mcbride/IdiomLite.pdf §2] M : Type → Type is equipped with pure : A → M A and seq : M (A → B) → M A → M B. Write 𝑓 <*> 𝑎 := seq 𝑓 𝑥<*> is left associative: 𝑢 <*> 𝑣 <*> 𝑤 = (𝑢 <*> 𝑣) <*> 𝑤. and 𝑎 *> 𝑏 := seq (_ ↦ 𝑎) 𝑏. Applicative functors obey the laws given in (2.12).

2.2.3. Inductive datatypes

New inductive datatypes are defined with a GADT-like syntax (2.13).

List (X : Type) ::=
| nil
| cons (x : X) (l : List X)

In cases where it is obvious which constructor is being used, the tag names are suppressed. Function definitions with pattern matching use the syntax given in (2.14).

f : Bool + (X × Y) → ℕ
  | true           ↦ 3
  | false          ↦ 0
  |        (𝑥,  𝑦) ↦ 2

One can express inductive datatypes D as fixpoints of functors D = Fix P where Fix P := P (Fix P). Depending on the underlying category, Fix P may not exist for all PSmyth and Plotkin are the first to place some conditions on when the fixpoint exists [SP82], see Adámek et al for a survey [AMM18].[SP82]Smyth, Michael B; Plotkin, Gordon DThe category-theoretic solution of recursive domain equations (1982)SIAM Journal on Computinghttp://wrap.warwick.ac.uk/46312/1/WRAP_Smyth_cs-rr-014.pdf[AMM18]Adámek, Jiří; Milius, Stefan; Moss, Lawrence SFixed points of functors (2018)Journal of Logical and Algebraic Methods in Programminghttps://doi.org/10.1016/j.jlamp.2017.11.003.

Definition 2.15 (base functor): When a D : Type is written as Fix P for some P (and there is no Q such that P = Q ∘ Q ∘ ... ∘ Q), P is called the base functor for D. This conceptualisation is useful because we can use the base functor to make related types without needing to explicitly write down the constructors for the modified versions. For example we can make the list lazy with Lazy P X := Fix ((X ↦ Unit → X) ∘ P).

2.3. Inductive gadgets

For the rest of this thesis, I will make use of a few motifs for discussing inductive datastructures, particularly in Section 2.4, Chapter 3, Appendix A and Appendix C. In this section I will lay some background material for working with inductive datatypes.

2.3.1. Traversable functors

Given a monad M, a common task is performing a monad-map with f : A → M B over a list of objects l : List X. This is done with the help of a function called mmap (2.16).

mmap (𝑓 : A → M B)
  : List A → M (List B)
  | []     ↦ pure []
  | (ℎ::𝑙) ↦ pure cons <*> 𝑓 ℎ <*> mmap 𝑓 𝑙

But we can generalise List to some functor T : Type → Type; when can we equip an analogous mmap to T? For example, in the case of binary trees (2.17).

Tree A ::=
| leaf   : Tree A
| branch : Tree A → A → Tree A → Tree A

mmap (𝑓 : A → M B)
   : Tree A         → M (Tree B)
   | leaf           ↦ pure leaf
   | (branch 𝑙 𝑎 𝑟) ↦
        pure branch <*> mmap 𝑓 𝑙 <*> 𝑓 𝑎 <*> mmap 𝑓 𝑟

Definition 2.18 (traversable): A functor T : Type → Type is traversable when for all applicative functors (Definition 2.11) M : Type → Type, there is a natural function d[M] : (T ∘ M) ⇒ (M ∘ T). That is, for each X : Type we have d[M][X] : T (M X) → M (T X). In addition to being natural, d must obey the traversal laws given in (2.19) [JR12[JR12]Jaskelioff, Mauro; Rypacek, OndrejAn Investigation of the Laws of Traversals (2012)Proceedings Fourth Workshop on Mathematically Structured Functional Programming, MSFP@ETAPS 2012, Tallinn, Estoniahttps://doi.org/10.4204/EPTCS.76.5 Definition 3.3].

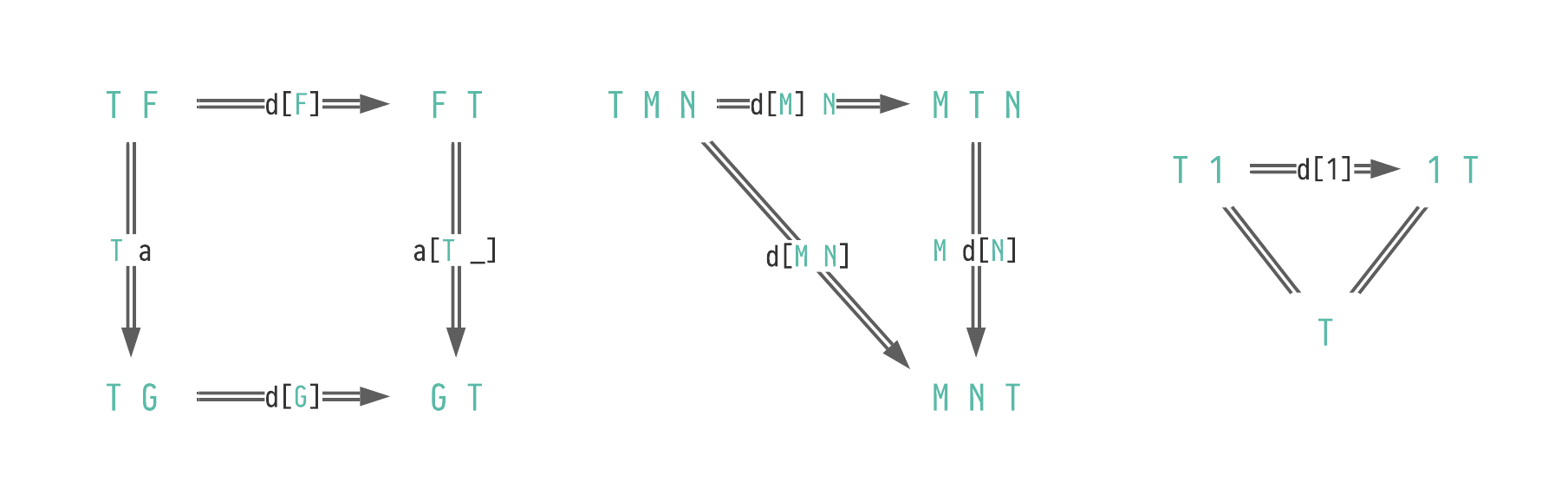
Given a traversable functor T and a monad M, we can recover mmap : (A → M B) → T A → M (T B) as mmap 𝑓 𝑡 := d[M][B] (T 𝑓 𝑡).

2.3.2. Functors with coordinates

Bird et al [BGM+13[BGM+13]Bird, Richard; Gibbons, Jeremy; Mehner, Stefan; et al.Understanding idiomatic traversals backwards and forwards (2013)Proceedings of the 2013 ACM SIGPLAN symposium on Haskellhttps://lirias.kuleuven.be/retrieve/237812] prove that (in the category of sets) the traversable functors are equivalent to a class of functors called finitary containers. Their theorem states that there is a type Shape T 𝑛 : TypeAn explicit definition of Shape T 𝑛 is the pullback of children[1] : T Unit ⟶ List Unit and !𝑛 : Unit ⟶ List Unit, the list with 𝑛 elements. for each traversable T and 𝑛 : ℕ such that that each 𝑡 : T X is isomorphic to an object called a finitary container on Shape T shown in (2.20).

T X ≅
    (length   : ℕ)
  × (shape    : Shape T length)
  × (children : Vec length X)

map and traverse may be defined for the finitary container as map and traverse over the children vector. Since 𝑡 : T X has 𝑡.length child elements, the children of 𝑡 can be indexed by the numbers {𝑘 : ℕ | 𝑘 < length}. We can then define operations to get and set individual elements according to this index 𝑘.

Usually, however, this numerical indexing of the children of 𝑡 : T X loses the semantics of the datatype. As an example; consider the case of a binary tree Tree in (2.21). A tree 𝑡 : Tree X with 𝑛 branch components will have length 𝑛 and a corresponding children : Vec 𝑛 X, but indexing via numerical indices {𝑘 | 𝑘 < 𝑛} loses information about where the particular child 𝑥 : X can be found in the tree.

TreeBase A X ::=
| leaf   : TreeBase X
| branch : TreeBase X → A → TreeBase X → TreeBase X

Tree A := Fix (TreeBase A)

Now I will introduce a new way of indexing the members of children for the purpose of reasoning about inductive datatypes. This idea has been used and noted before many times, the main one being paths in universal algebra [BN98[BN98]Baader, Franz; Nipkow, TobiasTerm rewriting and all that (1998)publisher Cambridge University Presshttps://doi.org/10.1017/CBO9781139172752 Dfn. 3.1.3]. However, I have not seen an explicit account of this idea in the general setting of traversable functors and later to general inductive datatypes (Section 2.3.3).

Definition 2.22 (coordinates): A traversable functor T has coordinates when equipped with a type C : Type and a function coords[𝑛] : Shape T 𝑛 → Vec 𝑛 C. The coords function amounts to a labelling of the 𝑛 children of a particular shape with members of C.

Often when using traversals, working with the children list Vec (length 𝑡) X for each shape of T can become unwieldy, so it is convenient to instead explicitly provide a pair of functions get and set (2.23) for manipulating particular children of a given 𝑡 : T X.

get : C → T X → Option X
set : C → T X → X → T X

get 𝑐 𝑡 = if ∃ 𝑖, (coords 𝑡)[𝑖] = 𝑐
          then some 𝑡.children[𝑖]
          else none

set 𝑐 𝑡 𝑥 = if ∃ 𝑖, (coords 𝑡)[𝑖] = 𝑐
            then Vec.set 𝑖 𝑡.children 𝑥
            else 𝑡

C is not unique, and in general should be chosen to have some semantic value for thinking about the structure of T. Here are some examples of functors with coordinates:

• List has coordinates ℕ. coords 𝑙 for 𝑙 : List X returns a list [0, ⋯, 𝑙.length - 1]. get 𝑖 𝑙 is some 𝑙[𝑖] and set 𝑖 𝑙 𝑥 returns a new list with the 𝑖th element set to be 𝑥.

• Vec n, lists of length n, has coordinates {k : ℕ | k < n} with the same methods as for List above.

• Option has coordinates Unit. coords (some 𝑥) := [()] and coords none := []. get _ 𝑜 := 𝑜 and set replaces the value of the option.

• Binary trees have coordinates List D as shown in (2.24).

D ::= | left | right

coords
  : Tree X       → List (List D)
  | leaf         ↦ []
  | branch 𝑙 𝑥 𝑟 ↦
    [ ..[[left, ..𝑐] for 𝑐 in coords 𝑙]
    , []
    , ..[[right , ..𝑐] for 𝑐 in coords 𝑟]
    ]

get : List (List Bool) → Tree X       → Option X
    | _                ↦ leaf         ↦ none
    | []               ↦ branch 𝑙 𝑥 𝑟 ↦ some 𝑥
    | [left, ..𝑐]      ↦ branch 𝑙 𝑥 𝑟 ↦ get 𝑐 𝑙
    | [right , ..𝑐]    ↦ branch 𝑙 𝑥 𝑟 ↦ get 𝑐 𝑟

2.3.3. Coordinates on initial algebras of traversable functors

Given a functor F with coordinates C, we can induce coordinates on the free monad Free F : Type → Type of F. The free monad is defined concretely in (2.25).

Free F X ::=
| pure : X → Free F X
| make : F(Free F X) → Free F X

join : (Free F (Free F X)) → Free F X
     | pure 𝑥 ↦ pure 𝑥
     | (make 𝑓) ↦ make (F join 𝑓)

We can write Free F X as the fixpoint of A ↦ X + F AAs mentioned in Section 2.2.3, these fixpoints may not exist. However for the purposes of this thesis the Fs of interest are always polynomial functors.. Free F has coordinates List C with methods defined in (2.26).

coords : Free F X → List (List C)
       | pure 𝑥   ↦ []
       | make 𝑓   ↦
         [ [𝑐, ..𝑎]
           for 𝑎 in coords (get 𝑐 𝑓)
           for 𝑐 in coords 𝑓]

get : List C   → Free F X → Option X
    | []       ↦ pure 𝑥   ↦ some 𝑥
    | [𝑐, ..𝑎] ↦ make 𝑓   ↦ (get 𝑐 𝑓) >>= get 𝑎
    | _        ↦ _        ↦ none

set : List C   → Free F X → X → Free F X
    | []       ↦ pure _   ↦ 𝑥 ↦ pure 𝑥
    | [𝑐, ..𝑎] ↦ make 𝑓   ↦ 𝑥 ↦ (set 𝑐   𝑓)
    | _        ↦ _        ↦ none

In a similar manner, List C can be used to reference particular subtrees of an inductive datatype D which is the fixpoint of a traversable functor D = F D. Let F have coordinates C. D here is not a functor, but we can similarly define coords : D → List (List C), get : List C → Option D and set : List C → D → D → D.

The advantage of using coordinates over some other system such as optics [FGM+07[FGM+07]Foster, J Nathan; Greenwald, Michael B; Moore, Jonathan T; et al.Combinators for bidirectional tree transformations: A linguistic approach to the view-update problem (2007)ACM Transactions on Programming Languages and Systems (TOPLAS)https://hal.inria.fr/inria-00484971/file/lenses-toplas-final.pdf] or other apparati for working with datatypes [LP03[LP03]Lämmel, Ralf; Peyton Jones, SimonScrap Your Boilerplate (2003)Programming Languages and Systems, First Asian Symposium, APLAS 2003, Beijing, China, November 27-29, 2003, Proceedingshttps://doi.org/10.1007/978-3-540-40018-9_23] is that they are much simpler to reason about. A coordinate is just an address of a particular subtree. Another advantage is that the choice of C can convey some semantics on what the coordinate is referencing (for example, C = left | right in (2.24)), which can be lost in other ways of manipulating datastructures.

2.4. Metavariables

Now with a way of talking about logical foundations, we can resume from Section 2.1.2 and consider the problem of how to represent partially constructed terms and proofs given a foundation. This is the purpose of a development calculus: to take some logical system $\mathcal{L}$ and produce some new system $D\mathcal{L}$ such that one can incrementally build terms and proofs in a way that provides feedback at intermediate points and ensures that various judgements hold for these intermediate terms. In Chapter 3, I will create a new development calculus for building human-like proofs, and in Appendix A this system will be connected to Lean. First we look at how Lean's current development calculus behaves. Since I will be using Lean 3 in this thesis and performing various operations over its expressions, I will follow the same general setup as is used in Lean 3. The design presented here was first developed by Spiwack [Spi11[Spi11]Spiwack, ArnaudVerified computing in homological algebra, a journey exploring the power and limits of dependent type theory (2011)PhD thesis (INRIA)https://pastel.archives-ouvertes.fr/pastel-00605836/document] first released in Coq 8.5. It was built to allow for a type-safe treatment of creating tactics with metavariables in a dependently-typed foundation.

2.4.1. Expressions and types

In this section I will introduce the expression foundation language that will be used for the remainder of the thesis. The system presented here is typical of expression structures found in DTT-based provers such as Lean 3 and Coq. I will not go into detail on induction schema and other advanced features because the work in this thesis is independent of them.

Definition 2.27 (expression): A Lean expression is a recursive datastructure Expr defined in (2.28).

ExprBase X ::=
| lambda : Binder → X → ExprBase X -- function abstraction
| pi : Binder → X → ExprBase X     -- dependent function type
| var : Name → ExprBase X           -- variables
| const : Name → ExprBase X         -- constants
| app : X → X → ExprBase X         -- function application
| sort : Level → ExprBase X         -- type universe

Binder := (name : Name) × (type : Expr)

Context := List Binder

Expr := Fix ExprBase

In (2.28), Level can be thought of as expressions over some signature that evaluate to natural numbers. They are used to stratify Lean's types so that one can avoid Girard's paradox [Hur95[Hur95]Hurkens, Antonius J. C.A simplification of Girard's paradox (1995)International Conference on Typed Lambda Calculi and Applicationshttps://doi.org/10.1007/BFb0014058]. Name is a type of easily distinguishable identifiers; in the case of Lean Names are lists of strings or numbers. I sugar lambda 𝑥 α 𝑏 as λ (𝑥 ∶ α), 𝑏, pi 𝑥 α 𝑏 as Π (𝑥 ∶ α), 𝑏, app 𝑓 𝑎 as 𝑓 𝑎 and omit var and const when it is clear what the appropriate constructor is.

Using ExprBase, define pure expressions Expr := Fix ExprBase as in Section 2.2.3. Note that it is important to distinguish between the meta-level type system introduced in Section 2.2 and the object-level type system where the 'types' are merely instances of ExprThis distinction can always be deduced from syntax, but to give a subtle indication of this distinction, object-level type assignment statements such as (𝑥 ∶ α) are annotated with a slightly smaller variant of the colon ∶ as opposed to : which is used for meta-level statements.. That is, 𝑡 : Expr is a meta-level statement indicating that 𝑡 is an expression, but ⊢ 𝑡 ∶ α is an object-level judgement about expressions stating that 𝑡 has the type α, where α : Expr and ⊢ α ∶ sort.

Definition 2.29 (variable binding): Variables may be bound by λ and Π expressions. For example, in λ (𝑥 ∶ α), 𝑡, we say that the expression binds 𝑥 in 𝑡. If 𝑡 contains variables that are not bound, these are called free variables. Now, given a partial map σ : Name ⇀ Expr and a term 𝑡 : Expr, we define a substitution subst σ 𝑡 : Expr as in (2.30). This will be written as σ 𝑡 for brevity.

subst σ : Expr → Expr
        | var 𝑥   ↦ if 𝑥 ∈ dom σ then σ 𝑥 else 𝑥
        | 𝑒       ↦ ExprBase (subst σ) 𝑒

I will denote substitutions as a list of Name ↦ Expr pairs. For example, ⦃𝑥 ↦ 𝑡, 𝑦 ↦ 𝑠⦄ where 𝑥 𝑦 : Name are the variables which will be substituted for terms 𝑡 𝑠 : Expr respectively.

Substitution can easily lead to badly-formed expressions if there are variable naming clashes. I need only note here that we can always perform a renaming of variables in a given expression to avoid clashes upon substitution. These clashes are usually avoided within prover implementations with the help of de-Bruijn indexing [deB72].

2.4.2. Assignable datatypes

Given an expression structure Expr and 𝑡 : Expr, we can define a traversal over all of the immediate subexpressions of 𝑡.

child_traverse (M : Monad) (𝑓 : Context → Expr → M Expr)
  : Context → Expr                → M Expr
  | Γ         ↦ (Expr.var 𝑛)        ↦ (Expr.var 𝑛)
  | Γ         ↦ (Expr.app 𝑙 𝑟)      ↦
    pure (Expr.app) <*> 𝑓 Γ 𝑙 <*> 𝑓 Γ 𝑟
  | Γ         ↦ (Expr.lambda 𝑛 α 𝑏) ↦
    pure (Expr.lambda 𝑛) <*> 𝑓 Γ α <*> 𝑓 [..Γ, (𝑛:α)] 𝑏

The function child_traverse defined in (2.31) is different from a normal traversal of a datatructure because the mapping function 𝑓 is also passed a context Γ indicating the current variable context of the subexpression. Thus when exploring a λ-binder, 𝑓 can take into account the modified context. This means that we can define context-aware expression manipulating tools such as counting the number of free variables in an expression (fv in (2.32)).

instantiate : Name → Expr → Context → Expr → Expr
| 𝑥 ↦ 𝑟 ↦ Γ ↦ (Expr.var 𝑛) ↦ if (𝑥 = 𝑛) then 𝑟 else Expr.var 𝑛
| 𝑥 ↦ 𝑟 ↦ Γ ↦ 𝑡            ↦ child_traverse 𝟙 (instantiate 𝑥 𝑟) Γ 𝑡

fv : Context → Expr → Set Name
| Γ ↦ (Expr.var 𝑛) ↦ if 𝑛 ∈ Γ then ∅ else {𝑛}
| Γ ↦ 𝑡            ↦ child_traverse Set (fv) Γ 𝑡

The idea here is to generalise child_traverse to include any datatype that may involve expressions. Frequently when building systems for proving, one has to make custom datastructures. For example, one might wish to create a 'rewrite-rule' structure (2.33) for modelling equational reasoning (as will be done in Chapter 4).

RewriteRule := (lhs : Expr) × (rhs : Expr)

Definition 2.34 (telescope): Another example might be a telescope of binders Δ : List Binder a list of binders is defined as a telescope in Γ : Context when each successive binder is defined in the context of the binders before it. That is, [] is a telescope and [(𝑥∶α), ..Δ] is a telescope in Γ if Δ is a telescope in [..Γ, (𝑥∶α)] and Γ ⊢ 𝑥 ∶ α.

But now if we want to perform a variable instantiation or count the number of free variables present in 𝑟 : RewriteRule, we have to write custom definitions to do this. The usual traversal functions from Section 2.3.1 are not adequate for telescopes, because we may need to take into account a binder structure. Traversing a telescope as a simple list of names and expressions will produce the wrong output for fv, because some of the variables are bound by previous binders in the context.

Definition 2.35 (assignable): To avoid having to write all of this boilerplate, let's make a typeclass assignable (2.36) on datatypes that we need to manipulate the expressions in. The expr_traverse method in (2.36) traverses over the child expressions of a datatype (e.g., the lhs and rhs of a RewriteRule or the type expressions in a telescope). expr_traverse also includes a Context object to enable traversal of child expressions which may be in a different context to the parent datatype.

class assignable (X : Type) :=
(expr_traverse :
  (M : Monad) →
  (Context → Expr → M Expr) →
  Context → X → M X
)

expr_traverse M 𝑓
  : Context → RewriteRule → RewriteRule
  | Γ         ↦ (𝑙, 𝑟)    ↦ do
    𝑙' ← 𝑓 Γ 𝑙;
    𝑟' ← 𝑓 Γ 𝑟;
    pure ⟨𝑙, 𝑟⟩

expr_traverse M 𝑓
  : Context → Telescope → Telescope
  | Γ       ↦ []        ↦ pure []
  | Γ       ↦ [(𝑥∶α), ..Δ] ↦ do
    α' ← 𝑓 Γ α;
    Δ' ← expr_traverse M 𝑓 [..Γ, (𝑥∶α)] Δ;
    pure [(𝑥∶α'), ..Δ']

Now, provided expr_traverse is defined for X: fv, instantiate and other expression-manipulating operations such as those in (2.32) can be modified to use expr_traverse instead of child_traverse. This assignable regime becomes useful when using de-Bruijn indices to represent bound variables [deB72] because the length of Γ can be used to determine the binder depth of the current expression. Examples of implementations of assignable and expression-manipulating operations that can make use of assignable can be found in my Lean implementation of this concepthttps://github.com/leanprover-community/mathlib/pull/5719.

2.4.3. Lean's development calculus

In the Lean source code, there are constructors for Expr other than those in (2.30). Some are for convenience or efficiency reasons (such as Lean 3 macros), but others are part of the Lean development calculus. The main development calculus construction is mvar or a metavariable, sometimes also called a existential variable or schematic variable. An mvar ?m acts as a 'hole' for an expression to be placed in later. There is no kernel machinery to guarantee that an expression containing a metavariable is correct; instead, they are used for the process of building expressions.

As an example, suppose that we needed to prove P ∧ Q for some propositions P Q ∶ Prop. The metavariable-based approach to proving this would be to declare a new metavariable ?𝑡 ∶ P ∧ Q. Then, a prover constructs a proof term for P ∧ Q in two steps; declare two new metavariables ?𝑡₁ ∶ P and ?𝑡₂ ∶ Q; and then assign ?𝑡 with the expression and.make ?𝑡₁ ?𝑡₂ where and.make ∶ P → Q → P ∧ Q is the constructor for ∧. After this, ?𝑡₁ and ?𝑡₂ themselves are assigned with p ∶ P and q ∶ Q. In this way, the proof term can be built up slowly as ?𝑡 ⟿ and.make ?𝑡₁ ?𝑡₂ ⟿ and.make p ?𝑡₂ ⟿ and.make p q. This process is more convenient for building modular programs that construct proofs than requiring that a pure proof term be made all in one go because a partially constructed proof is represented as a proof term where certain subexpressions are metavariables.

Lean comes with a development calculus that uses metavariables. This section can be viewed as a more detailed version of the account originally given by de Moura et al [MAKR15[MAKR15]de Moura, Leonardo; Avigad, Jeremy; Kong, Soonho; et al.Elaboration in Dependent Type Theory (2015)CoRRhttp://arxiv.org/abs/1505.04324 §3.2] with the additional details sourced from inspecting the Lean source code. Lean's metavariable management system makes use of a stateful global 'metavariable context' with carefully formed rules governing valid assignments of metavariables. While all automated provers make use of some form of metavariables, this specific approach to managing them for use with tactics was first introduced in Spiwack's thesis [Spi11], where the tactic monad for Coq was augmented with a stateful global metavariable context.

The implementation of Lean allows another Expr constructor for metavariables:

Expr ::=
| ExprBase Expr
| ?Name

Metavariables are 'expression holes' and are denoted as ?𝑥 where 𝑥 : Name. They are placeholders into which we promise to substitute a valid pure expression later. Similarly to fv(𝑡) being the free variables in 𝑡 : Expr, we can define mv(𝑡) to be the set of metavariables present in 𝑡. However, we still need to be able to typecheck and reduce expressions involving metavariables and so we need to have some additional structure on the context.

The idea is that in addition to a local context Γ, expressions are inspected and created within the scope of a second context called the metavariable context 𝑀 : MvarContext. The metavariable context is a dictionary MvarContext := Name ⇀ MvarDecl where each metavariable declaration 𝑑 : MvarDecl has the following information:

• identifier : Name A unique identifier for the metavariable.

• type : Expr The type of the metavariable.

• context : Context The local context of the metavariable. This determines the set of local variables that the metavariable is allowed to depend on.

• assignment : Option Expr An optional assignment expression. If assignment is not none, we say that the metavariable is assigned.

The metavariable context can be used to typecheck an expression containing metavariables by assigning each occurrence ?𝑥 with the type given by the corresponding declaration 𝑀[𝑥].type in 𝑀. The assignment field of MvarDecl is used to perform instantiation. We can interpret 𝑀 as a substitution.

As mentioned in Section 2.1.2, the purpose of the development calculus is to represent a partially constructed proof or term. The kernel does not need to check expressions in the development calculus (which here means expressions containing metavariables), so there is no need to ensure that an expression using metavariables is sound in the sense that declaring and assigning metavariables will be compatible with some set of inference rules such as those given in (2.4). However, in Appendix A.1, I will provide some inference rules for typing expressions containing metavariables to assist in showing that the system introduced in Chapter 3 is compatible with Lean.

2.4.4. Tactics

A partially constructed proof or term in Lean is represented as a TacticState object. For our purposes, this can be considered as holding the following data:

TacticState :=
    (result : Expr)
  × (mctx : MvarContext)
  × (goals : List Expr)

Tactic (A : Type) := TacticState → Option (TacticState × A)

The result field is the final expression that will be returned when the tactic completes. goals is a list of metavariables that are used to denote what the tactic state is currently 'focussing on'. Both goals and result are in the context of mctx.

Tactics may perform actions such as modifying the goals or performing assignments of metavariables. In this way, a user may interactively build a proof object by issuing a stream of tactics.

2.5. Understandability and confidence

This section is a short survey of literature on what it means for a mathematical proof to be understandable. This is used in Chapter 6 to evaluate my software and to motivate the design of the software in Chapter 3 and Chapter 4.

2.5.1. Understandability of mathematics in a broader context

What does it mean for a proof to be understandable? An early answer to this question comes from the 19th century philosopher Spinoza. Spinoza [Spi87[Spi87]Spinoza, BenedictThe chief works of Benedict de Spinoza (1887)publisher Chiswick Presshttps://books.google.co.uk/books?id=tnl09KVEd2UC&ots=WiBRHdjSjY&dq=the%20philosophy%20of%20benedict%20spinoza&lr&pg=PA3#v=onepage&q&f=false] supposes 'four levels' of a student's understanding of a given mathematical principle or rule, which are:

1. mechanical: The student has learnt a recipe to solve the problem, but no more than that.

2. inductive: The student has verified the correctness of the rule in a few concrete cases.

3. rational: The student comprehends a proof of the rule and so can see why it is true generally.

4. intuitive: The student is so familiar and immersed in the rule that they cannot comprehend it not being true.

For the purposes of this thesis I will restrict my attention to type 3 understanding. That is, how the student digests a proof of a general result. If the student is at level 4, and treats the result like a fish treats water, then there seems to be little an ITP system can offer other than perhaps forcing any surprising counterexamples to arise when the student attempts to formalise it.

Edwina Michener's Understanding Understanding Mathematics [Mic78[Mic78]Michener, Edwina RisslandUnderstanding understanding mathematics (1978)Cognitive sciencehttps://onlinelibrary.wiley.com/doi/pdf/10.1207/s15516709cog0204_3] provides a wide ontology of methods for understanding mathematics. Michener (p. 373) proposes that "understanding is a complementary process to problem solving" and incorporates Spinoza's 4-level model. She also references Poincaré's thoughts on understanding [Poi14[Poi14]Poincaré, HenriScience and method (1914)publisher Amazon (out of copyright)https://archive.org/details/sciencemethod00poinuoft p. 118], from which I will take an extended quote from the original:

What is understanding? Has the word the same meaning for everybody? Does understanding the demonstration of a theorem consist in examining each of the syllogisms of which it is composed and being convinced that it is correct and conforms to the rules of the game? ...

Yes, for some it is; when they have arrived at the conviction, they will say, I understand. But not for the majority... They want to know not only whether the syllogisms are correct, but why there are linked together in one order rather than in another. As long as they appear to them engendered by caprice, and not by an intelligence constantly conscious of the end to be attained, they do not think they have understood.

In a similar spirit; de Millo, Lipton and Perlis [MUP79[MUP79]de Millo, Richard A; Upton, Richard J; Perlis, Alan JSocial processes and proofs of theorems and programs (1979)Communications of the ACMhttps://doi.org/10.1145/359104.359106] write referring directly to the nascent field of program verification (here referred to 'proofs of software')

Mathematical proofs increase our confidence in the truth of mathematical statements only after they have been subjected to the social mechanisms of the mathematical community. These same mechanisms doom the so-called proofs of software, the long formal verifications that correspond, not to the working mathematical proof, but to the imaginary logical structure that the mathematician conjures up to describe his feeling of belief. Verifications are not messages; a person who ran out into the hall to communicate his latest verification would rapidly find himself a social pariah. Verifications cannot really be read; a reader can flay himself through one of the shorter ones by dint of heroic effort, but that's not reading. Being unreadable and - literally - unspeakable, verifications cannot be internalized, transformed, generalized, used, connected to other disciplines, and eventually incorporated into a community consciousness. They cannot acquire credibility gradually, as a mathematical theorem does; one either believes them blindly, as a pure act of faith, or not at all.

Poincaré's concern is that a verified proof is not sufficient for understanding. De Millo et al question whether a verified proof is a proof at all! Even if a result has been technically proven, mathematicians care about the structure and ideas behind the proof itself. If this were not the case, then it would be difficult to explain why new proofs of known results are valued by mathematicians. I explore the question of what exactly they value in Chapter 6.

Many studies investigating mathematical understanding within an educational context exist, see the work of Sierpinska [Sie90[Sie90]Sierpinska, AnnaSome remarks on understanding in mathematics (1990)For the learning of mathematicshttps://www.flm-journal.org/Articles/43489F40454C8B2E06F334CC13CCA8.pdf, Sie94[Sie94]Sierpinska, AnnaUnderstanding in mathematics (1994)publisher Psychology Presshttps://books.google.co.uk/books?id=WWu_OVPY7dQC] for a summary. See also Pólya's manual on the same topic [Pól62[Pól62]Pólya, GeorgeMathematical Discovery (1962)publisher John Wiley & Sonshttps://archive.org/details/GeorgePolyaMathematicalDiscovery].

2.5.2. Confidence

Another line of inquiry suggested by Poincaré's quote is distinguishing confidence in a proof from a proof being understandable. By confidence in a proof, I do not mean confidence in the result being true, but instead confidence in the given script actually being a valid proof of the result.

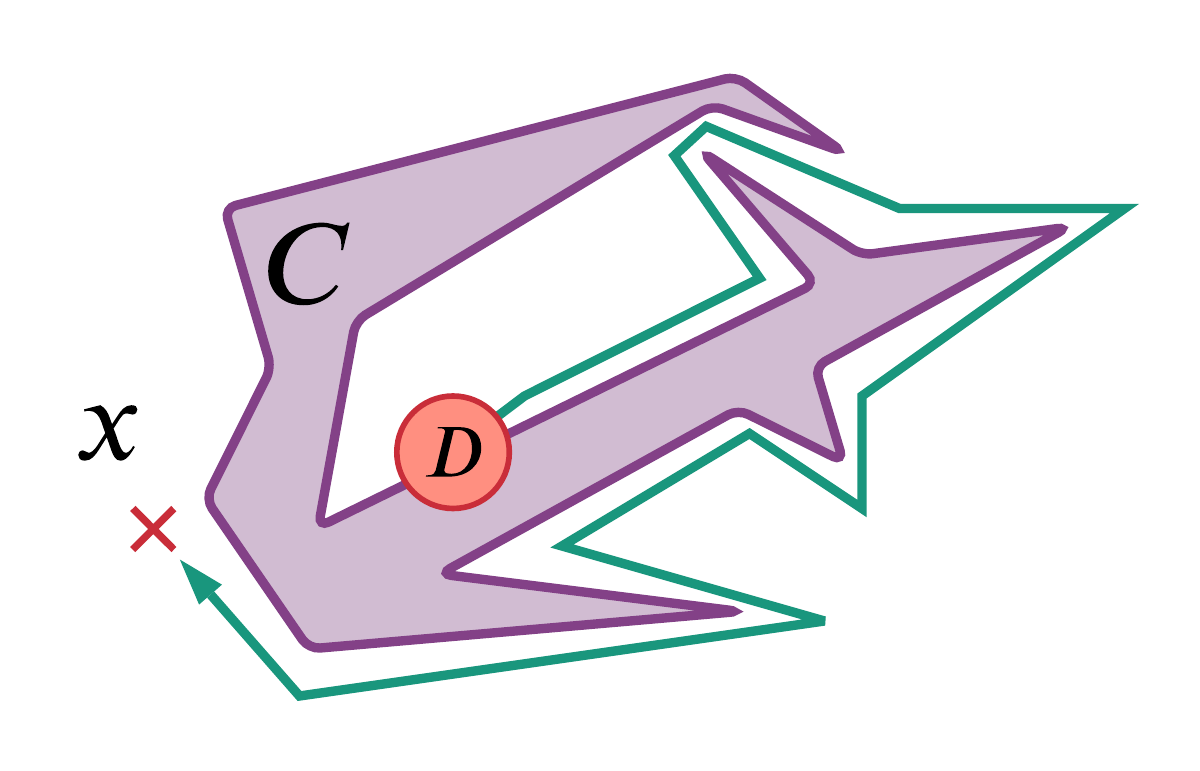
As an illustrative example, I will give my own impressions on some proofs of the Jordan curve theorem which states that any non-intersecting continuous loop in the 2D Euclidean plane has an interior region and an exterior region. Formal and informal proofs of this theorem are discussed by Hales [Hal07[Hal07]Hales, Thomas CThe Jordan curve theorem, formally and informally (2007)The American Mathematical Monthlyhttps://www.maths.ed.ac.uk/~v1ranick/papers/hales3.pdf]. I am confident that the proof of the Jordan curve theorem formalised by Hales in the HOL Light proof assistant is correct although I can't claim to understand it in full. Contrast this with the diagrammatic proof sketch (Figure 2.39) given in Hales' paper (originating with Thomassen [Tho92[Tho92]Thomassen, CarstenThe Jordan-Schönflies theorem and the classification of surfaces (1992)The American Mathematical Monthlyhttps://www.jstor.org/stable/2324180]). This sketch is more understandable to me but I am less confident in it being a correct proof (e.g., maybe there is some curious fractal curve that causes the diagrammatic proofs to stop being obvious...). In the special case of the curve $C$ being a polygon, the proof involves "walking along a simple polygonal arc (close to $C$ but not intersecting $C$)" and Hales notes:

Nobody doubts the correctness of this argument. Every mathematician knows how to walk without running in to walls. Detailed figures indicating how to "walk along a simple polygonal arc" would be superfluous, if not downright insulting. Yet, it is quite another matter altogether to train a computer to run around a maze-like polygon without collisions...

These observations demonstrate how one's confidence in a mathematical result is not merely a formal affair, but includes ostensibly informal arguments of correctness. This corroborates the attitude taken by De Millo et al in Section 2.5.1. Additionally, as noted in Section 1.1, confidence in results also includes a social component: a mathematician will be more confident that a result is correct if that result is well established within the field.

There has also been some empirical work on the question of confidence in proofs. Inglis and Alcock [QED[QED]Inglis, Matthew; Alcock, LaraExpert and novice approaches to reading mathematical proofs (2012)Journal for Research in Mathematics Educationhttps://pdfs.semanticscholar.org/494e/7981ee892d500139708e53901d6260bd83b1.pdf] performed an empirical study on eye movements in undergrads vs postgrads. A set of undergraduates and post-graduate researchers were presented with a set of natural language proofs and then asked to judge the validity of these proofs. The main outcomes they suggest from their work are that mathematicians can disagree about the validity of even short proofs and that post-graduates read proofs in a different way to undergraduates: moving their focus back and forth more. This suggests that we might expect undergraduates and postgraduates to present different reasons for their confidence in the questions.

2.5.3. Understandability and confidence within automated theorem proving.

The concepts of understandability and confidence have also been studied empirically within the context of proof assistants. This will be picked up in Chapter 6.

Stenning et al. [SCO95[SCO95]Stenning, Keith; Cox, Richard; Oberlander, JonContrasting the cognitive effects of graphical and sentential logic teaching: reasoning, representation and individual differences (1995)Language and Cognitive Processeshttp://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.49.3906&rep=rep1&type=pdf] used the graphical Hyperproof software (also discussed in Section 5.1) to compare graphical and sentence-based representations in the teaching of logic. They found that both representations had similar transferabilityThat is, do lessons learnt in one domain transfer to anologous problems in other domains? The psychological literature identifies this as a difficult problem in teaching. and that the best teaching representation (in terms of test scores) was largely dependent on the individual differences between the students. This suggests that in looking for what it means for a proof to be understandable, we should not forget that people have different ways of thinking about proofs, and so there is not going to be a one-size-fits-all solution. It also suggests that providing multiple ways of conceptualising problems should help with understandability.

In Grebing's thesis [Gre19[Gre19]Grebing, Sarah CaeciliaUser Interaction in Deductive Interactive Program Verification (2019)PhD thesis (Karlsruhe Institute of Technology)https://d-nb.info/1198309989/34], a set of focus group studies are conducted to ask a set of users with a variety of experience-levels in Isabelle and KeY, to reflect on the user interfaces. One of her main findings was that due to the extensive levels of automation in the proving process, there can arise a 'gap' between the user's model of the proof state and the proof state created through the automation. Grebing then provides a bridge for this gap in the form of a proof scripting language and user interface for the KeY prover at a higher level of abstraction than the existing interface. Grebing also provides a review of other empirical studies conducted on the user interfaces of proof assistants [Gre19 §6.2.0].

2.6. Human-like reasoning

How should a prover work to produce human-like mathematical reasoning? The easiest answer is: however humans think it should reason!

The very earliest provers such as the Boyer-Moore theorem prover [BM73[BM73]Boyer, Robert S.; Moore, J. StrotherProving Theorems about LISP Functions (1973)IJCAIhttp://ijcai.org/Proceedings/73/Papers/053.pdf, BM90[BM90]Boyer, Robert S; Moore, J StrotherA theorem prover for a computational logic (1990)International Conference on Automated Deductionhttps://www.cs.utexas.edu/users/boyer/ftp/cli-reports/054.pdf, BKM95[BKM95]Boyer, Robert S; Kaufmann, Matt; Moore, J StrotherThe Boyer-Moore theorem prover and its interactive enhancement (1995)Computers & Mathematics with Applications] take this approach to some extent; the design is steered through a process of introspection on how the authors would prove theorems. Nevertheless, with their 'waterfall' architecture, the main purpose is to prove theorems automatically, rather than creating proofs that a human could follow. Indeed Robinson's machine-like resolution method [BG01[BG01]Bachmair, Leo; Ganzinger, HaraldResolution theorem proving (2001)Handbook of automated reasoninghttps://www.sciencedirect.com/book/9780444508133/handbook-of-automated-reasoning] was such a dominant approach that Bledsoe titled his paper non-resolution theorem proving [Ble81[Ble81]Bledsoe, Woodrow WNon-resolution theorem proving (1981)Readings in Artificial Intelligencehttps://doi.org/10.1016/0004-3702(77)90012-1]. In this paper, Bledsoe sought to show another side of automated theorem proving through a review of alternative methods to resolution. A quote from this paper stands out for our current study:

It was in trying to prove a rather simple theorem in set theory by paramodulation and resolution, where the program was experiencing a great deal of difficulty, that we became convinced that we were on the wrong track. The addition of a few semantically oriented rewrite rules and subgoaling procedures made the proof of this theorem, as well as similar theorems in elementary set theory, very easy for the computer. Put simply: the computer was not doing what the human would do in proving this theorem. When we instructed it to proceed in a "human-like" way, it easily succeeded. Other researchers were having similar experiences.

This quote captures the concept of 'human-like' that I want to explore. Some piece of automation is 'human-like' when it doesn't get stuck in a way that a human would not.

Another early work on human-oriented reasoning is that of Nevins [Nev74[Nev74]Nevins, Arthur JA human oriented logic for automatic theorem-proving (1974)Journal of the ACMhttps://doi.org/10.1145/321850.321858]. Similar to this thesis, Nevins is motivated by the desire to make proofs more understandable to mathematicians. Some examples of prover automation that are designed to perform steps that a human would take are grind for PVS [SORS01[SORS01]Shankar, Natarajan; Owre, Sam; Rushby, John M; et al.PVS prover guide (2001)Computer Science Laboratory, SRI International, Menlo Park, CAhttps://pvs.csl.sri.com/doc/pvs-prover-guide.pdf] and the waterfall algorithm in ACL2 [KMM13[KMM13]Kaufmann, Matt; Manolios, Panagiotis; Moore, J StrotherComputer-aided reasoning: ACL2 case studies (2013)publisher Springer].

All of the systems mentioned so far came very early in the history of computing, and had a miniscule proportion of the computing power available to us today. Today, the concern that a piece of automation may not find a solution in a human-like way or finds a circumlocuitous route to a proof is less of a concern because computers are much more powerful. However I think that the resource constraints that these early pioneers faced provides some clarity on why building human-like reasoning systems matters. The designers of these early systems were forced to introspect carefully on how they themselves were able to prove certain theorems without needing to perform a large amount of compute, and then incorporated these human-inspired insights in to their designs.

My own journey into this field started with reading the work of Gowers and Ganesalingam (G&G) in their Robot prover [GG17[GG17]Ganesalingam, Mohan; Gowers, W. T.A fully automatic theorem prover with human-style output (2017)Journal of Automated Reasoninghttps://doi.org/10.1007/s10817-016-9377-1]A working fork of this can be found at https://github.com/edayers/robotone.. G&G's motivation was to find a formal system that better represented the way that a human mathematician would solve a mathematics problem, demonstrating this through the ability to generate realistic natural-language write-ups of these proofs. The system made use of a natural-deduction style hierarchical proof-state with structural sharing. The inference rules (which they refer to as 'moves') on these states and the order in which they were invoked were carefully chosen through an introspective process. The advantage of this approach is that the resulting proofs could be used to produce convincing natural language write-ups of the proofs. However, the system was not formalised and was limited to the domains hard-coded in to the system. The work in this thesis is a reimagining of this system within a formalised ITP system.

A different approach to exploring human-like reasoning is by modelling the process of mathematical discourse. Pease, Cornelli, Martin, et al [CMM+17[CMM+17]Corneli, Joseph; Martin, Ursula; Murray-Rust, Dave; et al.Modelling the way mathematics is actually done (2017)Proceedings of the 5th ACM SIGPLAN International Workshop on Functional Art, Music, Modeling, and Designhttps://doi.org/10.1145/3122938.3122942, PLB+17[PLB+17]Pease, Alison; Lawrence, John; Budzynska, Katarzyna; et al.Lakatos-style collaborative mathematics through dialectical, structured and abstract argumentation (2017)Artificial Intelligencehttps://doi.org/10.1016/j.artint.2017.02.006] have investigated the use of graphical discourse models of mathematical reasoning. In this thesis, however I have restricted the scope to human-like methods for solving simple lemmas that can produce machine-checkable proofs.

Another key way in which humans reason is through the use of diagrams [Jam01[Jam01]Jamnik, MatejaMathematical Reasoning with Diagrams: From Intuition to Automation (2001)publisher CSLI Presshttps://www.amazon.co.uk/gp/product/1575863235] and alternative representations of mathematical proofs. A prima facie unintuitive result such as $1+2+3+\cdots +n=\frac{1}{2}n(n+1)$ snaps together when presented with the appropriate representation in Figure 2.40. Jamnik's previous work explores how one can perform automated reasoning like this in the domain of diagrams Some recent work investigating and automating this process is the rep2rep project [RSS+20]. This is an important feature of general human-like reasoning, however in the name of scope management I will not explore representations further in this thesis.

2.6.1. Levels of abstraction

There have been many previous works which add higher-level abstraction layers atop an existing prover with the aim of making a prover that is more human-like.

Archer et al. developed the TAME system for the PVS prover [AH97[AH97]Archer, Myla; Heitmeyer, ConstanceHuman-style theorem proving using PVS (1997)International Conference on Theorem Proving in Higher Order Logicshttps://doi.org/10.1007/BFb0028384]. Although they were focussed on proving facts about software rather than mathematics, the goals are similar: they wish to create software that produces proofs which are natural to humans. TAME makes use of a higher abstraction level. However, it is only applied to reasoning about timed automata and doesn't include a user study.

As part of the auto2 prover tactic for Isabelle, Zhan [Zha16[Zha16]Zhan, BohuaAUTO2, a saturation-based heuristic prover for higher-order logic (2016)International Conference on Interactive Theorem Provinghttps://doi.org/10.1007/978-3-319-43144-4_27] developed a high-level proof script syntax to guide the automation of auto2. A script takes the form of asserting several intermediate facts for the prover to prove before proving the main goal. This script is used to steer the auto2 prover towards proving the result. This contrasts with tactic-based proof and structural scripts (e.g. Isar [Wen99]) which are instead instructions for chaining together tactics. With the auto2 style script, it is possible to omit a lot of the detail that would be required by tactic-based scripts, since steps and intermediate goals that are easy for the automation to solve can be omitted entirely. A positive of this approach is that by being implemented within the Isabelle theorem prover, the results of auto2 are checked by a kernel. However it is not a design goal of auto2 to produce proofs that a human can read.

2.6.2. Proof planning

Proof planning originated with Bundy [Bun88[Bun88]Bundy, AlanThe use of explicit plans to guide inductive proofs (1988)International conference on automated deductionhttps://doi.org/10.1007/BFb0012826, Bun98[Bun98]Bundy, AlanProof Planning (1998)publisher University of Edinburgh, Department of Artificial Intelligencehttps://books.google.co.uk/books?id=h7hrHAAACAAJ] and is the application of performing a proof with respect to a high-level plan (e.g., I am going to perform induction then simplify terms) that is generated before low-level operations commence (performing induction, running simplification algorithms). The approach follows the general field of AI planning.

AI planning in its most general conception [KKY95[KKY95]Kambhampati, Subbarao; Knoblock, Craig A; Yang, QiangPlanning as refinement search: A unified framework for evaluating design tradeoffs in partial-order planning (1995)Artificial Intelligencehttps://doi.org/10.1016/0004-3702(94)00076-D] is the process of searching a graph G using plan-space rather than by searching it directly. In a typical planning system, each point in plan-space is a DAGDirected Acyclic Graph of objects called ground operators or methods, each of which has a mapping to paths in G. Each ground operator is equipped with predicates on the vertices of G called pre/post-conditions. Various AI planning methods such as GRAPHPLAN [BF97] can be employed to discover a partial ordering of these methods, which can then be used to construct a path in G. This procedure applied to the problem of finding proofs is proof planning. The main issue with proof planning [Bun02] is that it is difficult to identify sets of conditions and methods that do not cause the plan space to be too large or disconnected. However, in this thesis we are not trying to construct plans for entire proofs, but just to model the thought processes of humans when solving simple equalities. A comparison of the various proof planners is provided by Dennis, Jamnik and Pollet [DJP06].

Proof planning in the domain of finding equalities frequently involves a technique called rippling [BSV+93[BSV+93]Bundy, Alan; Stevens, Andrew; Van Harmelen, Frank; et al.Rippling: A heuristic for guiding inductive proofs (1993)Artificial Intelligencehttps://doi.org/10.1016/0004-3702(93)90079-Q, BBHI05[BBHI05]Bundy, Alan; Basin, David; Hutter, Dieter; et al.Rippling: meta-level guidance for mathematical reasoning (2005)publisher Cambridge University Presshttps://books.google.co.uk/books?id=dZzbL-lnjVEC], in which an expression is annotated with additional structure determined by the differences between the two sides of the equation that directs the rewriting process. The rippling algorithm captures some human intuitions about which parts of a rewriting expression are salient. In the system for equational rewriting I introduce in Chapter 4, I avoid using rippling because the techniques are tied to peforming induction.

Another technique associated with proof planning is the concept of proof critics [Ire92[Ire92]Ireland, AndrewThe use of planning critics in mechanizing inductive proofs (1992)International Conference on Logic for Programming Artificial Intelligence and Reasoninghttps://doi.org/10.1007/BFb0013060]. Proof critics are programs which take advantage of the information from a failed proof plan to construct a new, amended proof plan. An interactive version of proof critics has also been developed [IJR99]. In the work in Chapter 3, this concept of revising a proof based on a failure is used.

Another general AI system that will be relevant to this thesis is hierarchical task networks [MS99[MS99]Melis, Erica; Siekmann, JörgKnowledge-based proof planning (1999)Artificial Intelligencehttps://doi.org/10.1016/S0004-3702(99)00076-4, Tat77[Tat77]Tate, AustinGenerating project networks (1977)Proceedings of the 5th International Joint Conference on Artificial Intelligence.https://dl.acm.org/doi/abs/10.5555/1622943.1623021] which are used to drive the behaviour of artificial agents such as the ICARUS architecture [LCT08]. In a hierarchical task network, tasks are recursively refined into subtasks, which are then used to find fine-grained methods for achieving the original tasks, eventually bottoming out in atomic actions such as actuating a motor. HTNs naturally lend themselves to human-like reasoning, and I will make use of these in designing a hierarchical algorithm for performing equational reasoning.

2.7. Natural language for formal mathematics

In this section I will survey the background and related work on using natural language to generate proofs. The material in this chapter will be used in Section 3.6 and Chapter 6.

2.7.1. Natural language generation in a wider context

Data-to-text natural language generation (NLG) is a subfield of natural language processing (NLP) that focusses on the problem of computing intelligible natural language discourses and text from some non-textual object (without a human in the loop!). An example is producing an English description of the local weather forecast from meteorological data. NLG techniques can range from simple 'canned text' and 'mail-merge' applications right up to systems with aspirations of generality such as modern voice recognition in smartphones.

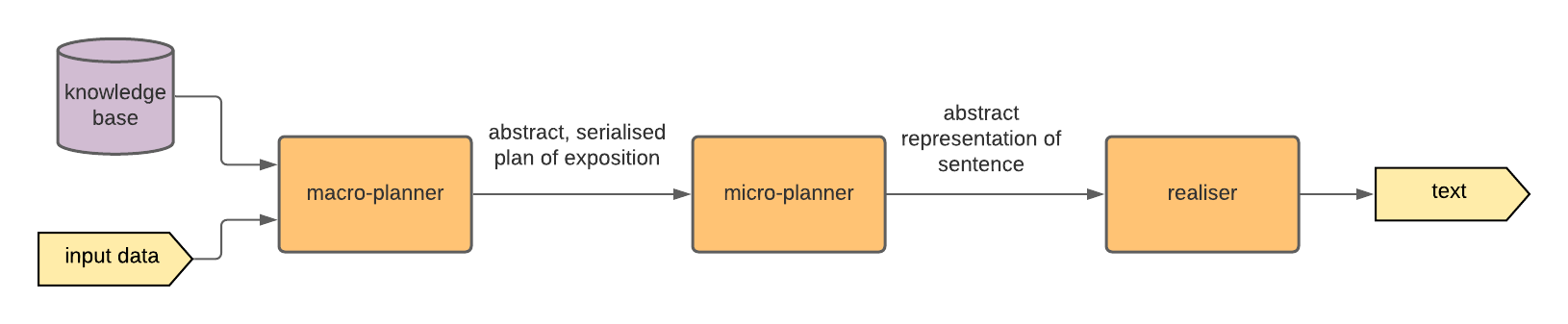
There are a wide variety of architectures available for modern NLG [GK18[GK18]Gatt, Albert; Krahmer, EmielSurvey of the state of the art in natural language generation: Core tasks, applications and evaluation (2018)Journal of Artificial Intelligence Researchhttps://doi.org/10.1613/jair.5477], however they usually carry a modular structure, with a backbone [RD00] being split in to three pipeline stages as shown in Figure 2.41.

[RD00]Reiter, Ehud; Dale, RobertBuilding natural language generation systems (2000)publisher Cambridge University Presshttps://dl.acm.org/doi/book/10.5555/331955

• Macro-planner or discourse planner: dictates how to structure the general flow of the text, that is, serialising the input data. These often take the form of 'expert systems' with a large amount of domain specific knowledge encoded.

• Micro-planner: determines how the stream of information from the macro-planner should be converted into individual sentences, how sentences should be structured and determining how the argument should 'flow'.

• Realiser: produces the final text from the abstracted output of the micro-planner, for example, applying punctuation rules and choosing the correct conjugations.

These choices of stages are mainly motivated through a desire to reuse code and to separate concerns (a realiser does not need to know the subject of the text it is correcting the punctuation from). I make use of this architecture in Section 3.6.

An alternative approach to the one outlined above is to use statistical methods for natural language generation. The advent of scalable machine learning (ML) and neural networks (NNs) of the 2010s has gained dominance in many NLG tasks such as translation and scene description. The system developed for this work in Section 3.6 is purely classical, with no machine learning component. In the context of producing simple write-ups of proofs, there will likely be some gains from including ML, but it is not clear that a statistical approach to NLG is going to assist in building understandable descriptions of proofs, because it is difficult to formally confirm that the resulting text generated by a black-box NLG component is going to accurately reflect the input.

2.7.2. Natural language generation for mathematics

The first modern study of the linguistics of natural language mathematics is the work of Ranta [Ran94[Ran94]Ranta, AarneSyntactic categories in the language of mathematics (1994)International Workshop on Types for Proofs and Programshttps://doi.org/10.1007/3-540-60579-7_9, Ran95[Ran95]Ranta, AarneContext-relative syntactic categories and the formalization of mathematical text (1995)International Workshop on Types for Proofs and Programshttps://doi.org/10.1007/3-540-61780-9_73] concerning the translation between dependent type theory and natural language and I will use some of his insights in Section 3.6. Ganesalingam's thesis [Gan10[Gan10]Ganesalingam, MohanThe language of mathematics (2010)PhD thesis (University of Cambridge)http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.211.9027&rep=rep1&type=pdf] is an excellent reference for understanding the linguistics of mathematics in general, however it is more concerned with natural language input.

There have been numerous previous attempts at creating natural language output from a theorem prover: Felty-Miller [FM87[FM87]Felty, Amy; Miller, DaleProof explanation and revision (1987)Technical Reporthttps://repository.upenn.edu/cgi/viewcontent.cgi?article=1660&context=cis_reports], Holland-Minkley et al within the NuPrl prover [HBC99[HBC99]Holland-Minkley, Amanda M; Barzilay, Regina; Constable, Robert LVerbalization of High-Level Formal Proofs. (1999)AAAI/IAAIhttp://www.aaai.org/Library/AAAI/1999/aaai99-041.php], and also in Theorema [BCJ+06[BCJ+06]Buchberger, Bruno; Crǎciun, Adrian; Jebelean, Tudor; et al.Theorema: Towards computer-aided mathematical theory exploration (2006)Journal of Applied Logichttps://doi.org/10.1016/j.jal.2005.10.006]. A particularly advanced NLG for provers was Proverb [HF97[HF97]Huang, Xiaorong; Fiedler, ArminProof Verbalization as an Application of NLG (1997)International Joint Conference on Artificial Intelligencehttp://ijcai.org/Proceedings/97-2/Papers/025.pdf] for the Ωmega theorem prover [BCF+97[BCF+97]Benzmüller, Christoph; Cheikhrouhou, Lassaad; Fehrer, Detlef; et al.Ωmega: Towards a mathematical assistant (1997)Automated Deduction - CADE-14https://doi.org/10.1007/3-540-63104-6_23], this system's architecture uses the pipeline in Figure 2.41 and takes as input a proof term generated by the Ωmega toolchain and outputs a natural language sentence. An issue with these generation tools is that their text will often produce text that does not appear natural at the macro-level. That is, the general structure of the argument will be different to what would be found in a mathematical textbook. G&G illustrate some examples of this in their paper [GG17 §2].

The process of synthesising natural language is difficult in the general case. But as G&G [GG17] note, the language found in mathematical proofs is much more restricted than a general English text. At its most basic, a natural language proof is little more than a string of facts from the assumptions to the conclusion. There is no need for time-sensitive tenses or other complexities that arise in general text. Proofs are written this way because mathematical proofs are written to be checked by a human and so a uniformity of prose is used that minimises the chance of 'bugs' creeping in. This, combined with a development calculus designed to encourage human-like proof steps, makes the problem of creating mathematical natural language write-ups much more tenable. I will refer to these non-machine-learning approaches as 'classical' NLG.

A related problem worth mentioning here is the reverse process of NLG: parsing formal proofs and theorem statements from a natural language text. The two problems are interlinked in that they are both operating on the same grammar and semantics, but parsing raises a distinct set of problems to NLG, particularly around ambiguity [Gan10 ch. 2]. Within mathematical parsing there are two approaches. The first approach is controlled natural language [Kuh14[Kuh14]Kuhn, TobiasA survey and classification of controlled natural languages (2014)Computational linguisticshttps://doi.org/10.1162/COLI_a_00168] as practiced by ForTheL [Pas07[Pas07]Paskevich, AndreiThe syntax and semantics of the ForTheL language (2007)PhD thesis (Université Paris XII)http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.211.8865&rep=rep1&type=pdf] and Naproche/SAD [CFK+09[CFK+09]Cramer, Marcos; Fisseni, Bernhard; Koepke, Peter; et al.The Naproche Project: Controlled Natural Language Proof Checking of Mathematical Texts (2009)Controlled Natural Language, Workshop on Controlled Natural Languagehttps://doi.org/10.1007/978-3-642-14418-9_11]. Here, a grammar is specified to parse text that is designed to look as close to a natural langauge version of the text as possible. The other approach (which I will not make use of in this thesis) is in using machine learning techniques, for example the work on parsing natural mathematical texts is in the work of Stathopoulos et al [ST16[ST16]Stathopoulos, Yiannos A; Teufel, SimoneMathematical information retrieval based on type embeddings and query expansion (2016)COLING 2016https://www.aclweb.org/anthology/C16-1221/, SBRT18[SBRT18]Stathopoulos, Yiannos; Baker, Simon; Rei, Marek; et al.Variable Typing: Assigning Meaning to Variables in Mathematical Text (2018)NAACL-HLT 2018https://doi.org/10.18653/v1/n18-1028].

In Section 3.6 I will make use of some ideas from natural language parsing, particularly the concept called notion by ForTheL and non-extensional type by Ganesalingam. A non-extensional type is a noun-phrase such as "element of a topological space" or "number" which is assigned to expressions, these types are not used by the underlying logical foundation but are used to parse mathematical text. To see why this is needed consider the syntax x y. This is parsed to an expression differently depending on the types of x and y (e.g., if x is a function vs. an element of a group). Non-extensional types allow this parse to be disambiguated even if the underlying foundational language does not have a concept of a type.

2.8. Chapter summary

In this chapter I have provided the necessary background information and prior work needed to frame the rest of the thesis. I have explained the general design of proof assistants (Section 2.1). I have described a meta-level pseudolanguage for constructing algorithms (Section 2.2) and provided some gadgets for working with inductive types within it (Section 2.3). I have also presented the philosophy and social aspects of understandability in mathematics (Section 2.5); human-like automated reasoning (Section 2.6); and natural language generation of mathematical text (Section 2.7).