This is a technical appendix on soundly running Lean tactics within a Box. It also provides some of the more technical background omitted from Section 2.4, such as the inference rules for the development calculus of Lean. In this I appendix I describe an 'escape-hatch' to use Lean tactics within a Box proof, meaning that we don't have to forgo using any prexisting tactic libraries by using the Box framework. Ultimately, these meta-level proofs are not critical to the thesis because the resulting object-level proofs produced through these box-tactics is also checked by the Lean kernel.

A.1. Typing of expressions containing metavariables

In this section I provide a set of formal judgements describing a theory of the metavariable system of Lean. When Lean typechecks a proof or term (described in Section 2.1), it is checked with respect to a dependent type theory called the calculus of constructions [CH88[CH88]Coquand, Thierry; Huet, Gérard P.The Calculus of Constructions (1988)Information and Computationhttps://doi.org/10.1016/0890-5401(88)90005-3]. However, Lean also allows terms to contain special variables called metavariables for producing partially constructed proofs. Background on metavariables is provided in Section 2.4. Although Lean's kernel does not check expressions containing metavariables, it is nevertheless important to have an understanding of the theory of metavariables to assist in creating valid expressions.

In this section I extend the Lean typing rules presented by Carneiro [Car19[Car19]Carneiro, MarioLean's Type Theory (2019)Masters' thesis (Carnegie Mellon University)https://github.com/digama0/lean-type-theory/releases/download/v1.0/main.pdf] to also handle typing judgements over expressions containing metavariables. These definitions are used in Appendix A.2 and Appendix A.3 to run Lean's native tactics within a Box context. I used the knowledge written in this section to implement an interface in the Lean 3 metaprogramming framework [EUR+17[EUR+17]Ebner, Gabriel; Ullrich, Sebastian; Roesch, Jared; et al.A metaprogramming framework for formal verification (2017)Proceedings of the ACM on Programming Languageshttps://doi.org/10.1145/3110278] for fine-grained control over the metavariable context.

The work in this section is not an original contribution, because de Moura and the other designers of Lean 3 had to produce this theory to create the software in the first place. To my knowledge, however, there is currently no place where the theory is written down in the same manner as Carneiro's work. There are also many accounts of the theories of development calculi similar to this [SH17[SH17]Sterling, Jonathan; Harper, RobertAlgebraic Foundations of Proof Refinement (2017)CoRRhttp://arxiv.org/abs/1703.05215, McB00[McB00]McBride, ConorDependently typed functional programs and their proofs (2000)PhD thesis (University of Edinburgh)http://hdl.handle.net/1842/374, Spi11[Spi11]Spiwack, ArnaudVerified computing in homological algebra, a journey exploring the power and limits of dependent type theory (2011)PhD thesis (INRIA)https://pastel.archives-ouvertes.fr/pastel-00605836/document]. I also do not offer a comprehensive account of the theory of Lean's development calculus, instead only including the parts that are needed to prove later results. The information in this section is gleaned from [EUR+17] and [MAKR15[MAKR15]de Moura, Leonardo; Avigad, Jeremy; Kong, Soonho; et al.Elaboration in Dependent Type Theory (2015)CoRRhttp://arxiv.org/abs/1505.04324], the sourcecode of the Lean 3 theorem prover and through many informal chats with the community on the leanprover Zulip server.

I start by repeating some definitions (A.1) that were given in Section 2.4. An explanation of the notation used in this appendix can be found in Section 2.2.

Binder := Name × Expr

Context := List Binder

Expr ::=
| app : Expr → Expr → Expr
| lam : Binder → Expr → Expr
| pi  : Binder → Expr → Expr
| var : Name → Expr
| mvar : Name → Expr
| const : Name → Expr
| sort : {Level} → Expr

MvarDecl :=
    (name       : Name)
  × (type       : Expr)
  × (ctx        : Context)
  × (assignment : Option Expr)

MvarContext := List MvarDecl

Let 𝑀 : MvarContext and Γ : Context. Binders are sugared as (𝑥 ∶ α)Note the use of a smaller colon ∶ for typing judgements vs : for meta-level type assignments. for ⟨𝑥, α⟩ : Binder. Unassigned MvarDecls (⟨𝑥, α, Γ, none⟩ : MvarDecl) are sugared as (Γ ⊢ ?𝑥 ∶ α) and assigned MvarDecls (⟨𝑥, α, Γ, some 𝑡⟩ : MvarDecl) are sugared as (Γ ⊢ ?𝑥 ∶ α ≔ 𝑡) (the Γ ⊢ may be omitted if not relevant). I use the convention that metavariable names always begin with question marks. Given 𝑥 : Name, write 𝑥 ∈ Γ when 𝑥 appears in Γ : Context.

To simplify analysis, I assume that all contexts do not include variable clashes. That is to say, there are no two binders with the same name in Γ or 𝑀. Since there are infinitely many variable names to choose from, these kinds of variable clashes can be avoided through renaming.

Each of the definitions in (A.1) are assignable as defined in Definition 2.35 in Section 2.4.2.

Definition A.2: Also define the following for 𝑟 : R where R is assignable.

• fv(𝑟) are the free variables in 𝑟.

• mv(𝑟) are the metavariables in 𝑟.

• umv(𝑀, 𝑟) are the unassigned metavariables in 𝑟 (according to context 𝑀).

• amv(𝑀, 𝑟) are the assigned metavariables in 𝑟.

Definition A.3 (substitution): In Definition 2.29, a substitution σ is defined as a partial map Sub := Name ⇀ Expr sending variable names to expressions. Given σ : Sub and an 𝑟 : R where R is assignable, σ 𝑟 replaces each variable in 𝑟 with the corresponding expression in σWith the usual caveats for variable clashes as noted in Definition 2.29. The notation for substitutions I use is ⦃𝑥 ↦ 𝑡⦄ where 𝑥 : Name is the variable to be substituted and 𝑡 : Expr is the replacement expressionThe reader may enjoy alist of substitution notations collected by Steele: https://youtu.be/dCuZkaaou0Q?t=1916.[Ste17]. Link to slides: http://groups.csail.mit.edu/mac/users/gjs/6.945/readings/Steele-MIT-April-2017.pdf.[Ste17]Steele Jr., Guy L.It's Time for a New Old Language (2017)http://2017.clojure-conj.org/guy-steele/. I extend this definition to include metavariable substitutions; ⦃?𝑚 ↦ 𝑡⦄ is the substitution replacing each instance of ?𝑚 with the expression 𝑡.

A metavariable context 𝑀 can be viewed as a substitution mapping ?𝑚 to 𝑡 for each assigned declaration ⟨?𝑚, α, Γ, some 𝑡⟩ ∈ 𝑀. That is, 𝑀 acts by replacing each instance of an assigned metavariable with its assignment.

Definition A.4 (instantiation): Given an assignable 𝑒, write 𝑀 𝑒 to be the 𝑀-instantiation of 𝑒, created by performing this substitution to 𝑒. 𝑒 is 𝑀-instantiated when all of the metavariables present in 𝑒 are unassigned with respect to 𝑀.

Definition A.5 (flat): Say that a metavariable context 𝑀 is flat when amv(𝑀, 𝑀) = ∅. That is, when there are no assigned metavariables in the expressions found in 𝑀.

Definition A.6 (dependency ordering): Given an assignable 𝑟, say that 𝑟 depends on ?𝑚 when ?𝑚 ∈ mv(𝑟). Given a pair of declarations 𝑑₁ = ⟨?𝑚₁, α₁, Γ₁, 𝑜₁⟩ and 𝑑₂ = ⟨?𝑚₂, α₂, Γ₂, 𝑜₂⟩ in 𝑀, write 𝑑₁ ▸ 𝑑₂ when 𝑑₂ depends on ?𝑚₁. That is 𝑑₁ ▸ 𝑑₂ when α₂ or Γ₂ or 𝑜₂ depend on ?𝑚₁. I will write ?𝑚₁ ▸ ?𝑚₂ as a shorthand for 𝑑₁ ▸ 𝑑₂ when it is clear what the declarations are from context.

Given the list of declarations 𝑀 : MvarContext as vertices, ▸ forms a directed graph. Assuming that this graph is acyclic, there exists a topological ordering of the declarations. That is, there is an ordering of the declarations in 𝑀 such that each declaration only depends on earlier declarations.

Definition A.7 (well-formed context): This substitution operation on 𝑀 helps motivate the constraints that make a metavariable context well-formed. In particular, define 𝑀 to be well-formed when

• 𝑀's dependency graph is acyclic. For example, the metavariable declaration ⟨?𝑚, α, Γ, some ?𝑚⟩ assigning ?𝑚 to itself would cause a loop. More perniciously, the assignment could cause an infinitely growing term as in ⦃?𝑚 ↦ ?𝑚 + ?𝑚⦄. The no-loop property depends on the entire 𝑀, as we may have a multi-declaration dependency cycle such as ⦃?𝑚 ↦ f(?𝑛), ?𝑛 ↦ g(?𝑛)⦄.

• Performing 𝑀 on an expression 𝑡 : Expr (or other assignable object) should preserve the type of 𝑡 in a suitable context Γ. This requirement will be formalised in Appendix A.1.1 when typing judgements are introduced for expressions. To illustrate with some examples:

  • Performing ⦃?𝑚 ↦ "hello"⦄ to ?𝑚 + 4 would produce a badly typed expression "hello" + 4, so assignments must have the same type as their metavariables.

  • Performing ⦃?𝑚 ↦ 𝑥 + 2⦄ to ?𝑚 + (λ 𝑥, 𝑥 - ?𝑚) 5 will produce (𝑥 + 2) + (λ 𝑥, 𝑥 - (𝑥 + 2)) 5. But this is badly formed because the variable 𝑥 escapes the scope of its lambda binder. Hence there needs to be a way of making sure that a metavariable assignment can't depend on variables that would cause these malformed expressions. This is why the MvarDecl definition includes a context Γ for each declaration.

Definition A.8 (assign): Given a metavariable context 𝑀 with an unassigned metavariable ?𝑚 and a candidate expression 𝑡 : Expr, we need a way of updating 𝑀 so that ?𝑚 is assigned to 𝑡. Call this function assign : MvarContext → Name → Expr → Option MvarContext. The procedure of assign 𝑀 ?𝑚 𝑡 is as followsThe implementation in core Lean can be found at https://github.com/leanprover-community/lean/blob/05dd36d1717649932fccaafa0868321fb87f916d/src/library/type_context.cpp#L2175.:

1. Find the corresponding declaration ⟨?𝑚, α, Γ, none⟩ ∈ 𝑀. If it doesn't exist in 𝑀 or it is already assigned, fail by returning none.

2. Assert that instantiating ?𝑚 with 𝑣 does not introduce dependency cycles. That is, for each ?𝑥 ∈ mv(𝑀 𝑡) (𝑀 𝑡 is the 𝑀-instantiation of 𝑡), adding ?𝑥 ▸ ?𝑚 does not introduce a cycle to 𝑀's dependency graph.

3. Assert that typings and contexts are correct with 𝑀;Γ ⊢ 𝑡 ∶ α (to be defined in Appendix A.1.1).

4. Delete ?𝑚 from 𝑀.

5. Update 𝑀 to be ⦃?𝑚 ↦ 𝑀 𝑡⦄ 𝑀. That is, each occurrence of ?𝑚 in 𝑀 is replaced with the 𝑀-instantiation of 𝑡. Now ?𝑚 ∉ mv(𝑀).

6. Insert ⟨?𝑚, α Γ, some 𝑡⟩ into 𝑀.

Note that performing the assignment operation introduced in Definition A.8 causes the dependency ordering to change: for example supposing 𝑑₁ ▸ 𝑑₂ in 𝑀 and then if 𝑑₁ is assigned with a term 𝑡 not containing a metavariable, then 𝑑₂ will no longer depend on ?𝑚₁ and so 𝑑₁ ▸̷ 𝑑₂. An assignment may also cause a declaration to depend on metavariables that it did not previously depend on. As such, when an assignment is performed it may be necessary to reorder the declarations to recover the topological ordering. A reordering always exists, because step 2 of Definition A.8 ensures that the resulting metavariable context has no cycles.

Given 𝑀 : MvarContext, we will often be adding additional declarations and assignments to 𝑀 to make a new 𝑀 + Δ : MvarContext. Let's define Δ : MvarContextExtension as in (A.9).

MvarContextExtension ::=
| declare (mvar_name : Name) (type : Expr) (context : Context)
| assign (mvar_name : Name) (assignment : Expr)

extend : MvarContext → MvarContextExtension → MvarContext
| 𝑀 ↦ declare ?𝑚 α Γ ↦ [..𝑀, ⟨?𝑚, α, Γ, none⟩]
| 𝑀 ↦ assign ?𝑚 𝑣    ↦ assign 𝑀 ?𝑚 𝑣

In order for a declare ?𝑚 α Γ to be valid for 𝑀, require that 𝑀;Γ ⊢ α : Type and that ?𝑚 ∉ 𝑀. Then we have that performing a valid declaration preserves the acylicity of 𝑀 with respect to ▸. An assignment extension also preserves acyclicity; since step 2 of the procedure in Definition A.8 explicitly forbids dependency loops.

Hence, given a sequence of extensions to 𝑀, the ▸ relation is still acyclic and hence there exists a topological ordering of the declarations in 𝑀 for ▸.

A.1.1. Judgements and inference rules for metavariables

Now let's define the following judgements (in the same sense as in Section 2.1.3):

• 𝑀;Γ ⊢ 𝑠 ∶ α
  when 𝑠 has type α under 𝑀 and Γ.

• 𝑀;Γ ⊢ 𝑠 ≡ 𝑡
  when 𝑠 : Expr and 𝑡 : Expr are definitionally equal (see [Car19 §2.2]).

• ok 𝑀
  when the metavariable context 𝑀 is well-formed.

• 𝑀 ⊢ ok Γ
  when the given local context Γ is well-formed under 𝑀.

The inference rules for these are given in (A.10).

I'll reproduce the list of (non-inductive) typing axioms here for completeness, but please see Carneiro's thesis [Car19] for a more comprehensive version, including a full set of inference rules for let binders, reductions, definitional equality and inductive constructions among others.

[Hur95]Hurkens, Antonius J. C.A simplification of Girard's paradox (1995)International Conference on Typed Lambda Calculi and Applicationshttps://doi.org/10.1007/BFb0014058I now extend the above analysis to include an account of the metavariable development calculus that Lean uses to represent partially constructed proofs.

A.1.2. Properties of the Lean development calculus

In this subsection I note some regularity lemmas for the extended development calculus similarly to Carneiro [Car19 §3.2]. The first thing to note is that a judgement 𝑀;Γ ⊢ J is invariant under a reordering of the declarations of Γ or 𝑀 that preserves the dependency ordering.

Lemma A.13 (Γ-regularity): Using (A.10) and some additional rules for definitional equality (≡, not printed here) and inductive datatypes, Carneiro proves various properties of the type system, of which the following regularity lemmas are relevant for the analysis here:

• (Γ ⊢ 𝑒 ∶ α) ⇒ ⊢ Γ ok. If the context is not well formed, then we can't make any typing judgements.

• Γ ⊢ 𝑒 ∶ α ⇒ fv(𝑒) ⊆ Γ ∧ fv(α) ⊆ Γ. If a term is well typed in Γ then all of the free variables are present.

Proof: these lemmas are proven by induction on the premiss judgments; any ℎ : (Γ ⊢ 𝑒 ∶ α) must be constructed from one of the judgements in (A.10) and (A.11).

Lemma A.14 (𝑀-regularity): These regularity lemmas can be extended to include metavariables and a metavariable context 𝑀.

• (𝑀;Γ ⊢ 𝑡 ∶ α) ⇒ (⊢ 𝑀 ok)

• (𝑀;Γ ⊢ 𝑡 ∶ α) ⇒ (𝑀 ⊢ Γ ok)

• (𝑀;Γ ⊢ 𝑡 ∶ α) ⇒ mv(𝑡) ⊆ 𝑀

Proof: by applications of induction in a similar way to Lemma A.13.

Lemma A.15: The metavariables in 𝑀 are topologically ordered on ▸ (Definition A.6)

Proof: induction on ⊢ 𝑀 ok. Each successive declaration can't depend on those that precede it.

Lemma A.16: A well-formed (Definition A.7) metavariable context 𝑀 preserves typing judgements.

Proof: This follows from the congruence rule for ≡I.e., 𝑓₁ ≡ 𝑓₂ and 𝑎₁ ≡ 𝑎₂ imply 𝑓₁ 𝑎₁ ≡ 𝑓₂ 𝑎₂, see [Car19 §2.6]. and the assignment-eq rule in (A.11).

Lemma A.18: ⊢ 𝑀 ok ⇒ ⊢ (𝑀 𝑀) ok where 𝑀 𝑀 is the instantiation (Definition A.4) of 𝑀 with itself.

Proof: 𝑀 𝑀 is defined to be 𝑀 with every occurrence of the 𝑀-assigned metavariables replaced with itself. Hence through repeated applications of Lemma A.16, we have ⊢ (𝑀 𝑀) ok.

⊢ 𝑀 ok does not imply that 𝑀 is flat (Definition A.5), however any such 𝑀 with ⊢ 𝑀 ok can be flattened through repeated instantiation of 𝑀 on itself.

Lemma A.19: If ⊢ 𝑀 ok, then a finite number of self-instantiations of 𝑀 will be flat.

Proof: This follows from 𝑀's declarations being a topological ordering on ▸ (Lemma A.15). Let ⟨?𝑥, α, Γ, some 𝑡⟩ be an assignment in 𝑀. Then ?𝑚 ▸ ?𝑥 for all ?𝑚 ∈ mv(𝑡) by Definition A.6. Now, for any declaration 𝑑 ∈ 𝑀 where ?𝑥 ▸ 𝑑, we have ?𝑥 ▸̸ 𝑀 𝑑 and ?𝑚 ▸ 𝑀 𝑑 for all ?𝑚 ∈ mv(𝑡) since each occurrence of ?𝑥 in 𝑑 has been replaced with 𝑡. Hence after each instantiation of 𝑀, all declarations that depend on an assigned metavariable ?𝑥 will be replaced with declarations that depend on strictly earlier metavariables in the dependency ordering, and so by well-founded induction on ▸, eventually there will be no assigned metavariables in 𝑀ₙ.

Is it possible to create an 𝑀 such that there is a dependency (Definition A.6) cycle among the metavariable declarations in 𝑀? For example, can we declare a recursive pair of metavariables ?n : {i : ℕ | i ≤ ?m} and ?m : {i : ℕ | i ≤ ?n}? This follows from the typing rules (A.11) because a metavariable context is only ok when there is an explicit ordering on the metavariables such that each does not depend on the lastIn Lean's actual implementation, it is possible to do this through the tactic.unsafe.type_context monad using an unsafe assignment, in this case an infinite-descending expression will form which will not typecheck (because Lean's typechecker has a finite depth)..

However, in the definition of assign (Definition A.8), step 5 is to perform an update 𝑀 ↦ ⦃?𝑚 ↦ 𝑀 𝑣⦄ 𝑀. Note that ⊢ 𝑀 ok ⇏ ⊢ ⦃?𝑚 ↦ 𝑀 𝑣⦄ 𝑀 ok: set 𝑀 = [(?𝑚₁∶α),(?𝑚₂∶β(?𝑚₁),(?𝑚₃∶α))]; the resulting substitution ⦃?𝑚₁ ↦ ?𝑚₃⦄ sends 𝑀 to 𝑀' := [(?𝑚₁∶α),(?𝑚₂∶β(?𝑚₃)),(?𝑚₃∶α))] where now ?𝑚₃ ▸ ?𝑚₂ and so ⊬ 𝑀 ok. Fortunately, as noted after Definition A.8, there is a reordering π of declarations in 𝑀' which keeps the dependency ordering.

Lemma A.20: Assuming the conditions of assignment for assign 𝑀 ?𝑚 𝑣 hold (Definition A.8), there is a permutation π such that ⊢ π (⦃?𝑚 ↦ 𝑀 𝑣⦄ 𝑀) ok.

Proof: Let π be the topological ordering of (⦃?𝑚 ↦ 𝑀 𝑣⦄ 𝑀) with respect to ▸. This ordering exists by the 'no loops' assumption in Definition A.8. We can show ⊢ π (⦃?𝑚 ↦ 𝑀 𝑣⦄ 𝑀) ok by noting that every declaration 𝑑 ∈ 𝑀 has a corresponding ⦃?𝑚 ↦ 𝑀 𝑣⦄ 𝑑 ∈ 𝑀'. We can then perform induction on 𝑀'. Assuming that ⊢ 𝑀' ok, we have⊢ [..𝑀', ⦃?𝑚 ↦ 𝑀 𝑣⦄⟨?𝑏,β,B⟩] ok and need to show 𝑀';⦃?𝑚 ↦ 𝑀 𝑣⦄𝐵 ⊢ ⦃?𝑚 ↦ 𝑀 𝑣⦄β ∶ sort. By assign's second condition, we have 𝑀;Γ ⊢ 𝑣 : α, and so by a similar argument to Lemma A.16, we have that ⦃?𝑚 ↦ 𝑀 𝑣⦄ preserves typing judgements. It is also clear that typing judgements are preserved by reordering, provided that dependencies are respected.

Lemma A.21: The function assign 𝑀 ?𝑚 𝑣 (Definition A.8) with valid arguments preserves typing judgements. That is, the inference (A.17) holds.

Proof: WLOG we may assume that 𝑀 is flat. This is because instantiating preserves typing judgements by Lemma A.16 and repeated instantiation has a fixpoint by Lemma A.19. The result of performing the steps in Definition A.8 is that assign 𝑀 ?𝑚 𝑣 returns 𝑀 with the ?𝑚 declaration removed, each instance of ?𝑚 substituted with 𝑀 𝑣 and appended with ⟨?𝑚, α, Γ, 𝑣⟩. I will prove this by first showing that ⊢ (assign 𝑀 ?𝑚 𝑣) ok. We have that 𝑀₁ := ⦃?𝑚 ↦ 𝑀 𝑣⦄ 𝑀 does not introduce any dependency cycles by the 'no loops' condition, so reorder And so as noted in Lemma A.20, there exists a permutation 𝑀₂ := π 𝑀₁ of the declarations in 𝑀₁ such that ⊢ 𝑀₂ ok. We have that ?𝑥 ∉ mv(𝑀₂) (since 𝑀₂ is flat and ?𝑚 ∉ mv(𝑀 𝑣)), so we can remove the declaration for ?𝑥 in 𝑀₂ and append ⟨?𝑚, α, Γ, 𝑣⟩ without changing the validity. Hence ⊢ (assign 𝑀 ?𝑚 𝑣) ok. Finally, we can show (assign 𝑀 ?𝑚 𝑣);𝐵 ⊢ 𝑏 ∶ β by induction on the declarations in 𝑀₃ := (assign 𝑀 ?𝑚 𝑣). The metavariables in 𝑀₃ are the same as those in 𝑀, so it suffices to show that 𝑀;E ⊢ 𝑡 : γ ⇒ 𝑀₃;E ⊢ 𝑡 : γ for all 𝑡, γ, E. Which can be shown by noting that the substitution ⦃?𝑚 ↦ 𝑀 𝑣⦄ preserves typing judgements.

A.2. Zippers on Boxes

In order to run Lean tactics at various points in the Box structure defined in Chapter 3, we need to navigate to a certain point in a Box, and build up a metavariable context 𝑀 containing all of the metavariables from the 𝒢-binders and a local context Γ comprising the variables given in the ℐ-binders above the given point in the Box. The way to implement this plan is to define a context-aware zipper [Hue97[Hue97]Huet, GérardFunctional Pearl: The Zipper (1997)Journal of functional programminghttp://www.st.cs.uni-sb.de/edu/seminare/2005/advanced-fp/docs/huet-zipper.pdf] on a Box.

Let's first create a coordinate system for Box. Coordinates for functors and inductive datatypes were introduced in Section 2.3.2.

Coord ::=
| ℐ | 𝒢 | 𝒱 | 𝒜₁ | 𝒜₂ | 𝒪₁ | 𝒪₂

Address := List Coord

Where here 𝒜₁ is the coordinate for the b₁ argument of the 𝒜 constructor. That is, get 𝒜₁ (𝒜 𝑏₁ 𝑥 𝑏₂) = some 𝑏₁. Similarly for the other coordinates. Definition A.24: A list of Coord instances can be interpreted as an address to a certain point in an expression (see Section 2.3.3).

Definition A.25 (zipper): Next, define a datastructure called a path (using the same constructor names as Boxes) as shown in (A.26). A zipper is a tuple consisting of a Path and a Box.

PathItem ::=
| ℐ  : Binder → PathItem
| 𝒢  : Binder → PathItem
| 𝒱  : Binder → Expr → PathItem
| 𝒜₁ : Unit → Binder → Box  → PathItem
| 𝒜₂ : Box  → Binder → Unit → PathItem
| 𝒪₁ : Unit → Box  → PathItem
| 𝒪₂ : Box  → Unit → PathItem

Path := List PathItem

Zipper :=
  (path : Path)
× (cursor : Box)

We can visualise the zipper as in Figure A.27: a Box is annotated with an additional blob of paint ⬤ at some point in the tree. The ancestors of ⬤ are in the zipper's path, and everything below is the cursor.

h₁ : P → R

---

𝑕₁ : P

---

?𝑡₁: R

𝑕₂ : Q

---

⬤

?𝑡₂: R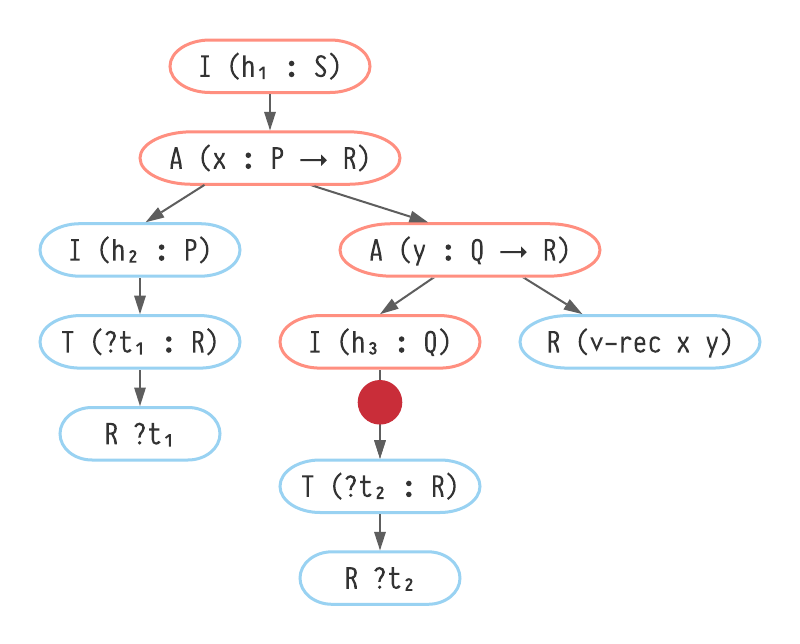

On the zipper, we can perform the up : Zipper → Option Zipper and down : Coord → Zipper → Option Zipper operations as defined in (A.28) and (A.29). Applying up to this zipper will move the ⬤ up to the next node in the Box tree (or return none otherwise). Similarly, down 𝑐 𝑧 (A.26) will inspect the cursor of 𝑧 and move the ⬤ down on its 𝑐th recursive argument. The use of a zipper datastructure is used over an address for ⬤ because the zipper system allows us to modify the cursor in place and then 'unzip' the zipper to perform an operation on a sub-box.

unwrap : Coord → Box → Option (PathItem × Box)
       | ℐ  ↦ ℐ (𝑥∶α)    𝑏  ↦ some (ℐ (𝑥∶α)       , 𝑏 )
       | 𝒢  ↦ 𝒢 (?𝑚:α)   𝑏  ↦ some (𝒢 ?𝑚          , 𝑏 )
       | 𝒱  ↦ 𝒱 (𝑥∶α) 𝑣  𝑏  ↦ some (𝒱 (𝑥∶α) 𝑣     , 𝑏 )
       | 𝒜₁ ↦ 𝒜 𝑏₁ (𝑥∶α) 𝑏₂ ↦ some (𝒜₁ () (𝑥∶α) 𝑏₂, 𝑏₁)
       | 𝒜₂ ↦ 𝒜 𝑏₁ (𝑥∶α) 𝑏₂ ↦ some (𝒜₂ 𝑏₁ (𝑥∶α) (), 𝑏₂)
       | 𝒪₁ ↦ 𝒪 𝑏₁       𝑏₂ ↦ some (𝒪₁ ()       𝑏₂, 𝑏₁)
       | 𝒪₂ ↦ 𝒪 𝑏₁       𝑏₂ ↦ some (𝒪₂ 𝑏₁       (), 𝑏₂)

wrap : PathItem → Box → Box
     | ℐ (𝑥∶α)        ↦ 𝑏  ↦ ℐ (𝑥∶α)    𝑏
     | 𝒢 ?𝑚           ↦ 𝑏  ↦ 𝒢 (?𝑚:α)   𝑏
     | 𝒱 (𝑥∶α) 𝑣      ↦ 𝑏  ↦ 𝒱 (𝑥∶α) 𝑣  𝑏
     | 𝒜₁ () (𝑥∶α) 𝑏₂ ↦ 𝑏₁ ↦ 𝒜 𝑏₁ (𝑥∶α) 𝑏₂
     | 𝒜₂ 𝑏₁ (𝑥∶α) () ↦ 𝑏₂ ↦ 𝒜 𝑏₁ (𝑥∶α) 𝑏₂
     | 𝒪₁ ()       𝑏₂ ↦ 𝑏₁ ↦ 𝒪 𝑏₁       𝑏₂
     | 𝒪₂ 𝑏₁       () ↦ 𝑏₂ ↦ 𝒪 𝑏₁       𝑏₂

up : Zipper        → Option Zipper
   | ⟨[],       𝑏⟩ ↦ none
   | ⟨[..𝑝, 𝑖], 𝑏⟩ ↦ some ⟨𝑝, wrap 𝑖 𝑏⟩

down : Coord → Zipper → Option Zipper
     | 𝑐     ↦ ⟨𝑝, 𝑏⟩ ↦ do
       ⟨𝑖, 𝑏₂⟩ ← (unwrap 𝑐 𝑏)
       pure ⟨[..𝑝, 𝑖], 𝑏₂⟩

down : List Coord → Zipper → Option Zipper
     | []         ↦ 𝑧      ↦ some 𝑧
     | [𝑐, ..𝑎]   ↦ 𝑧      ↦ down 𝑐 𝑧 >>= down 𝑎

unzip : Zipper → Box
| ⟨[], 𝑏⟩ ↦ 𝑏
| ⟨[..𝑝, 𝑖], 𝑏⟩ ↦ unzip ⟨𝑝, wrap 𝑖 𝑏⟩

zip : Box → Zipper
    | b   ↦ ⟨∅, [], b⟩

Motivated by Figure A.27, it may be readily verified that down 𝑐 (up 𝑧) = some 𝑧 provided 𝑧's path is not empty and if 𝑐 is the coordinate corresponding to 𝑧's rightmost path entry. With similar conditions: up (down 𝑐 𝑧) = some 𝑧.

Definition A.30 (zipper contexts): Define the context of a zipper 𝑧.ctx as:

ctx : PathItem  → Context
    | ℐ 𝑥       ↦ [𝑥]
    | 𝒜₂ 𝑏₁ 𝑥 _ ↦ [𝑥]
    | _         ↦ []

ctx : Zipper  → Context
    | ⟨_,𝑝,_⟩ ↦ [..(ctx 𝑥) for 𝑥 in 𝑝]

That is, 𝑧.ctx returns the list of the variables that are bound in the path. For the example 𝑧 in Figure A.27, 𝑧.ctx = [h₁].

Similarly, define the metavariable context 𝑧.mctx of a zipper as

mctx : PathItem → List Binder
     | 𝒢 𝑚      ↦ [𝑚]
     | _        ↦ []

mctx : Zipper → MvarContext
     | ⟨_,𝑝,_⟩  ↦ {..(mctx 𝑥) for 𝑥 in 𝑝}

So 𝑧.mctx is a metavariable context containing all of the goals defined above the cursor of 𝑧.

Now, given a zipper 𝑧, write 𝑧 ⊢ 𝑡 ∶ α to mean 𝑧.mctx;𝑧.ctx ⊢ 𝑡 ∶ α. Similarly for 𝑝 : Path, 𝑝 ⊢ 𝑡 ∶ α.

Lemma A.33 (zipping is sound): Suppose that 𝑓 : MvarContext → Context → Box → Option Box is a sound box tactic parametrised by the contexts 𝑀 and Γ, then given 𝑏 : Box and a valid address 𝑎 : List Coord, we get another sound box-tactic 𝑓@𝑎 defined in (A.34).

𝑓@𝑎 : Box → Option Box
    | 𝑏₁  ↦ do
      ⟨𝑝, 𝑏₂⟩ ← down 𝑎 𝑏₁
      𝑏₃     ← 𝑓 𝑝.mctx 𝑝.ctx 𝑏₂
      pure (unzip ⟨𝑝, 𝑏₃⟩)

Proof: Suppose that ⊢ 𝑏₁ ∶ α, then by induction on the typing laws for Box given in Section 3.4.2, we can show 𝑝 ⊢ 𝑏₂ ∶ ζ for some ζ : Expr. Since 𝑓 is sound and assuming 𝑓(𝑏₂) doesn't fail, we also have 𝑝 ⊢ 𝑏₃ ∶ ζ. Then finally the typing laws Section 3.4.2 can be applied in reverse to recover ⊢ (unzip ⟨𝑝, 𝑧⟩) ∶ α.

Here we are working towards being able to soundly run a tactic in the context provided by a Box zipper 𝑧 by finding ways to manipulate zippers that preserve the inference rules given in (A.10) and (A.11). We also need to perform some modifications to the paths of Zippers.

Definition A.35 (path soundness): A path modification ρ : 𝑝 ↦ 𝑝' is sound on a zipper 𝑧 = ⟨𝑝, 𝑏⟩ if 𝑀;Γ ⊢ unzip ⟨𝑝, 𝑏⟩ ∶ β and 𝑀;Γ ⊢ unzip ⟨𝑝', 𝑏⟩ ∶ β. Hence to show soundness, one simply needs to show that corresponding box-tactic unzip ∘ ρ is sound.

We have the following sound path-based box-tactics:

A.3. Running tactics in Boxes

Now that we have the inference rules for metavariables and a definition of a zipper over a Box, we can define how to run a tactic within a Box.

Definition A.39 (hoisting 𝒪 boxes): Before defining how to make a tactic act on a Box zipper we need to define an additional operation, called 𝒪-hoisting. This is where an 𝒪-box is lifted above its parent box. This definition extends to 𝒪-hoisting path entries.

𝒪-lift
  : Box                ⇀ Box
  | (ℐ 𝑕 (𝒪 𝑏₁ 𝑏₂))    ↦ 𝒪 (ℐ 𝑕 𝑏₁) (ℐ 𝑕 𝑏₂)
  | (𝒢 𝑚 (𝒪 𝑏₁ 𝑏₂))    ↦ 𝒪 (𝒢 𝑚 𝑏₁) (𝒢 𝑚 𝑏₂)
  | (𝒜 𝑏₀ 𝑥 (𝒪 𝑏₁ 𝑏₂)) ↦ 𝒪 (𝒜 𝑏₀ 𝑥 𝑏₁) (𝒜 𝑏₀ 𝑥 𝑏₂)
  | (𝒜 (𝒪 𝑏₁ 𝑏₂) 𝑥 𝑏₀) ↦ 𝒪 (𝒜 𝑏₁ 𝑥 𝑏₀) (𝒜 𝑏₂ 𝑥 𝑏₀)
  | (𝒱 𝑥 𝑣 (𝒪 𝑏₁ 𝑏₂))  ↦ 𝒪 (𝒱 𝑥 𝑣 𝑏₁) (𝒱 𝑥 𝑣 𝑏₂)
  | _                  ↦ none

Lemma A.43: 𝒪-hoisting is a sound box-tactic.

Proof: by compatibility (Lemma 3.15) it suffices to show that the results are equal, but then this is a corollary of the WLOG proof from the compatibility lemma (3.17).

The motivation behind the hoisting is that 𝒪 boxes are a form of backtracking state in a similar spirit to a logic monad [KSFS05[KSFS05]Kiselyov, Oleg; Shan, Chung-chieh; Friedman, Daniel P; et al.Backtracking, interleaving, and terminating monad transformers: (functional pearl) (2005)ACM SIGPLAN Noticeshttps://doi.org/10.1145/1086365.1086390]. However by including the branching 𝒪 box on the tree, it is possible to structurally share any context that is shared among the backtracking branches. Hoisting an 𝒪 box has the effect of causing the backtracking branches to structurally share less of the context with each other. In the most extreme case, we can repeatedly apply 𝒪-hoisting to move all of the branches to the top of the box structure, at which point we arrive at something isomorphic to what would arise as a result of using the logic monad form of backtracking.

Given 𝑧 : Zipper, define 𝑧.goal to be first metavariable declared on 𝑧.path. Hence given a 𝑧 : Zipper with the cursor having shape 𝒢, we can extract a metavariable context 𝑀 = mctx 𝑧 and a special goal metavariable 𝑧.goal, from these, create 𝑡𝑠 : TacticStateSee Section 2.4.4.. We can now run a tactic 𝑡 : Tactic on 𝑡𝑠. If successful, this will return a new tactic state 𝑡𝑠'. 𝑡𝑠' will have an extension of 𝑀See (A.9)., call this 𝑀 + Δ where Δ is a list of declarations and assignments successively applied to 𝑀. The task here is to create a new 𝑧': Zipper which includes the new goals and assignments in Δ.

The crux of the task here is to use Δ to construct a new 𝑝' : Path such that unzipping ⟨𝑝', (M + Δ) 𝑧.cursor⟩ : Zipper will result in a sound box-tactic. In general, this will mean placing new metavariable declarations from Δ as new 𝒢 entries in the path and deleting 𝒢 entries which are assigned in Δ. Additionally, it may be necessary to hoist 𝒪 boxes and re-order existing 𝒢 entries. This has to be done carefully or else we can introduce ill-formed boxes.

For example, take the zipper shown in (A.44) with metavariable context 𝑀 containing one metavariable ?𝑚 : ℕ. There is a tactic apply List.length that will act on the goal ?𝑚 by declaring a pair of new metavariables ?α : sort and ?𝑙 : List ?α and assigning ?𝑚 with List.length ?𝑙. After perfroming this tactic, the new metavariable context 𝑀 + Δ is (A.45).

𝑀 + Δ = { ⟨?𝑚 := length ?𝑙, Γ⟩
        , ⟨?α, Type, Γ⟩
        , ⟨?𝑙, List ?α, Γ⟩
        }

But now if our 𝑧.path is [𝒢 (?𝑚 : ℕ)], unzipping ⟨[𝒢 (?𝑚 : ℕ)], (𝑀 + Δ) 𝑧.cursor⟩ (A.46) will not result in a valid 𝑏 : Box (i.e. one that we can derive a judgement ⊢ 𝑏 : β) because the result will depend on metavariables ?α and ?𝑙 which do not have corresponding 𝒢-binders.

We need to make sure that the new metavariables ?α and ?𝑙 are abstracted and added to the Path as shown in (A.47), so when we unzip we end up with a well-formed Box.

We can find additional complications if the tactic declares new metavariables in a context E other than the current local context Γ. This may happen as a result of calling intros or performing an induction step. In these cases, some additional work must be done to ensure that the newly declared metavariable is placed at the correct point in the Box such that the context produced by the path above it is the same as E. This is tackled in the next section through the definition of a function called update.

The procedure for correctly adjusting the path to produce valid boxes as exemplified by (A.47) is as follows. Define a function update : MvarContextExtension → Path → Option Path. Here, MvarContextExtension (see (A.9)) is either a metavariable assignment or a metavariable declaration for 𝑀.

Definition A.48 (update): update Δ 𝑝 is defined such that (update Δ 𝑝).mctx = extend Δ 𝑝.mctx where extend is defined in (A.9). To do this, update will either insert a new 𝒢 path entry or delete a 𝒢 according to whether Δ is a declaration or an assignment. Then it will reorder the 𝒢 declarations such that it respects the dependency ordering ▸.

In general, this is not always possible since there there may be a pair of declarations 𝑑₁ 𝑑₂ : MvarDecl such that 𝑑₁ ▸ 𝑑₂ but 𝑑₂.context ≤ 𝑑₁.context, and so there is not necessarily an ordering of the declarations which is topological on both ≤ and ▸. This case can be handled in theory through redeclaring metavariables and using delayed abstractions as I discuss in Appendix A.3.1, however I do not analyse or implement this case here because it arises rarely in practice: most of the newly declared metavariables will not be in a different context or in a subcontext of 𝑝.ctx. Furthermore most of the tactics which do cause complex declarations to appear such as intro have an equivalent box-tactic.

update : MvarContextExtension → Zipper → Option Zipper
update (declare ?𝑚 α Γ) ⟨𝑝,𝑏⟩ :=
  assert 𝑝.mctx;Γ ⊢ α ∶ sort
  if (Γ ≤ 𝑝.ctx):
    obtain E such that [..Γ, ..E] = 𝑝.ctx
    obtain [..𝑝₀, ..𝑝₁] = 𝑝 such that
      𝑝₀.ctx = Γ and 𝑝₀ ⊢ α ∶ sort
    𝑝 ← [..𝑝₀, 𝒢 ?𝑚∶α, ..𝑝₁]
    reorder 𝑝
    return ⟨𝑝, 𝑏⟩
  else if (Γ > 𝑝.ctx):
    obtain E such that [..𝑝.ctx, 𝑥₀, ..., 𝑥ₙ] = Γ
    𝑝 ← [..𝑝,  𝒜₂ (ℐ 𝑥₀ $ ... $ ℐ 𝑥ₙ $ 𝒢 ?𝑚) 𝑦]
    reassign ?𝑚 in 𝑏 with (?𝑚 𝑥₀ ... 𝑥ₙ)
    reorder 𝑝
    return ⟨𝑝,𝑏⟩
  else (Γ ≹ 𝑝.ctx):
    -- that is, Γ and 𝑝.ctx are incomparable
    fail -- this case is not supported

update (assign ?𝑚 𝑣) ⟨𝑝, 𝑏⟩ :=
  assert (𝑝.mctx.assign ?𝑚 𝑣) is valid
  delete (𝒢 ?𝑚) from 𝑝
  assign 𝑣 to ?𝑚 in 𝑝
  reorder 𝑝
  return 𝑝

Some remarks on (A.49):

• reorder 𝑝 performs a reordering on the 𝒢 binders in 𝑝 to respect ▸ and contexts. As noted earlier, in certain circumstances this may not be possible, in which case fail.

• To account for 𝒪-boxes: before performing the above reordering, liftAnalogously to (A.40). all 𝒪 items in 𝑝 so that the resulting ..𝑝₁ does not contain any 𝒪-binders.

• In the case that Δ = declare ?𝑚 α Γ and Γ ≤ 𝑝.ctx, I am making the assumption that α doesn't depend on any metavariables whose context is outside Γ. This can occur if the offending metavariable is wrapped in a delayed abstraction. I discuss this caveat in Appendix A.3.1.

• The case where Γ > 𝑝.ctx works by reassigning the newly declared metavariable ?𝑚 with it's skolemised version and wrapping the declaration in a series of ℐ boxes. A circumstance where this can occur is if the intros tactic was used. I do not analyse the soundness of this case in further detail because it is expected that in these cases the intro move on Boxes (3.25) should be used instead.

An example of performing the assign case of (A.49) is given in (A.50):

Suppose that a tactic assigned ?𝑡₁ with ?𝑡₃ + 4. Then without any reordering the box would look like (A.51):

However this is not a valid box because the 𝒢-binder for ?𝑡₂ depends on a variable that is not in scope. Fortunately as discussed in Lemma A.20 a total dependency ordering of metavariables in the same context always exists, and so in update we can use the 'goal-swap' (A.37) path-reordering box-tactic to rearrange the goals to obey this. This is performed in the reorder step in update (A.49).

The way that update is defined means that

• (update (declare ?𝑚 α Γ) 𝑧).mctx = extend (declare ?𝑚 α Γ) 𝑧.mctx for a valid declaration with Γ ≤ 𝑝.ctx (up to reordering of the declarations in 𝑧.mctx). As mentioned above, the other case Γ > 𝑝.ctx is not considered here. Let ⟨𝑝', 𝑏'⟩ = update (declare ?𝑚 α Γ) ⟨𝑝, 𝑏⟩ and 𝑝 ⊢ 𝑏 ∶ α. Then 𝑝' ⊢ 𝑏 ∶ α too because 𝑝'.ctx = 𝑝.ctx and 𝑝'.mctx = extend Δ 𝑝.mctx. And we saw in Appendix A.1.2 that adding a declaration to a metavariable context preserves type judgements.

• Similarly, we have (update (assign ?𝑚 𝑣) 𝑧).mctx = extend (assign ?𝑚 𝑣) 𝑧.mctx for a valid assignment. Now let ⟨𝑝', 𝑏'⟩ = update (assign ?𝑚 𝑣) ⟨𝑝, 𝑏⟩ and 𝑝 ⊢ 𝑏 ∶ α. Then similarly 𝑝' ⊢ ⦃?𝑚 ↦ 𝑣⦄ 𝑏 ∶ ⦃?𝑚 ↦ 𝑣⦄ α.

We can now put together the components Now let zz : Zipper → Zipper be some function that navigates to a certain point in a Box and let tac be a tactic, we can define the 'escape hatch' tactic procedure, depicted below in Figure A.52.

A.3.1. A variant of 𝒜 supporting delayed abstraction

A delayed abstraction 𝑒[𝑥] is a special type of expressionLean 3 calls it a delayed abstraction macro. constructed with a local variable 𝑥 and an expression 𝑒 which may depend on 𝑥. A delayed abstraction represents an abstraction of 𝑥 on 𝑒An abstraction is when free variables are replaced with bound variables.. This is used when 𝑒 depends on a metavariable ?𝑚 whose declaration context contains 𝑥. In this case, performing the abstraction immediately would be premature because the metavariable ?𝑚 might need to depend on 𝑥.

There are a few possible variants and extensions of the design of 𝒜 boxes which I considered. The main limitation of 𝒜 boxes as detailed above is that the structure of b₁ is inscrutable when zipped on b₂. So in the above example we could not infer the structure of the function through reasoning on b₂. In order to model this, it is necessary to invoke delayed abstractions.

To get this to work, when zipping to b₂, one needs to first zip to the final 𝒭 r in b₁, and then instantiate b₂ with a delayed abstraction of r. Then, when performing up 𝒜₂, if a metavariable under a delayed abstraction has been assigned you need to unzip back through the entirety of b₁ and add any new goals to the path. So a variant PathItem.𝒜₁ would change to Path → Expr → List Name → Expr.