In this appendix I will detail the algorithm used to create interactive, browser-renderable HTML from a user's implementation of a component.
The design of the algorithm is largely a simplified variant of the 'tree reconciliation' algorithm used in web-based FRP frameworks such as React and Elm.
The React reconciliation algorithm has been generalised many timesAn example is the react-three-fiber project which lets one build declarative scenegraphs for a 3D scene. https://docs.pmnd.rs/react-three-fiber and the algorithm has been documented on the React websitehttps://reactjs.org/docs/reconciliation.html.
I hope that this appendix will prove useful to people who wish to implement ProofWidgets for themselves.
The pseudocode language described in Section 2.2 will be used throughout to make the relevant parts as salient as possible. I'm going to first walk through a simple todo-list example to make the setting clear and concrete.
C.1. Motivating ProofWidgets with a todo list app
A first approximation to a user interface is as a way of rendering information. So suppose that we have some datatype M that we care about, for example M could be the list of items in a todo list. Then we could write a function view : M → UI to express the process of creating an image on the screen. The most general formulation of UI would be an image ℝ² → colour and indeed some FRP frameworks explore this [Ell01[Ell01]Elliott, ConalFunctional Image Synthesis (2001)Proceedings of Bridgeshttp://conal.net/papers/bridges2001/], however we will content ourselves with an abstract tree of HTML[I will call this abstract tree the DOM in accordance with Section 5.2 to be converted to pixels on a screen by a web-browser.
Attr A ::=| val (key : String) (value : String)| click (handler : Unit → A)Html A ::=| element (tag : String) (attrs : List (Attr A)) (children : List (Html A))| of_string (value : String)
So here the html <div id="x">hello</div> would be represented as element "div" [val "id" "x"] [of_string "hello"] : Html A.
However, let's keep using the XML style <div/> notation.
As before the A type is the action type and represents the type of objects that the tree can emit when the user interacts with it.
Now we can create a button as element "button" [click (() ↦ 3)] ["click me!"] : Html ℕ or <button click={() ↦ 3}>click me!</button>.
This emits the number 3 whenever the button is clicked.
As before, let's introduce Components. A Component : Type → Type → Type allows us to encapsulate state at a particular point in the tree.
of_component : Component P A → P → Html Apure : (P → Html A) → Component P Awith_state(init : P → S)(props_changed : P → P → S → S)(update : P → S → B → S × Option A)(c : Component (S × P) B): Component P Amap_action (A → B) : Html A → Html B := ... -- reader exercise
The arguments P and A are called the prop type and the action type.
The actions of a component perform the same role as with Html A, that is, they are the type of object that is returned when the user interacts with the UI in some way. The props are effectively the input arguments to the component.
The reason for including P as a type argument (instead of writing something representable like P → Component A) is that it allows the component to update the state in the case of the props changing. That is, it allows the component to model the input p : P as a stream of values to pull from rather than as a single value.
An example use of this is adding a custom check that the component needs to update; a component showing the contact information for a single student doesn't need to re-render when the entire database updates, only when the entry for that student changes.
So for example we can make a textbox using components:
namespace textboxAction ::=| add| text_change (s : String)State := Stringinit : Unit → String| () ↦ ""props_changed : Unit → Unit → State → State| () ↦ () ↦ 𝑠 ↦ 𝑠update : Unit → State → Action → (State × Option String)| () ↦ 𝑠 ↦ add ↦ ("", some 𝑠)| () ↦ 𝑠₀ ↦ text_change 𝑠₁ ↦ (𝑠₁, none)view : (State × Unit) → Html Actionview (𝑠, ()) :=<div><input type="text" onchange={𝑠₁ ↦ text_change 𝑠₁} value={𝑠}/><button click={() ↦ add}>+</button></div>comp : Component Unit String :=with_state Action State init props_changed update $ pure viewend textboxtextbox : Html String := of_component textbox.comp ()
The resulting textbox element contains some hidden state, namely the text content of the textbox before the "+" button is pressed.
We could then place this within a larger component such as a todolist:
TodoItem := (label : String) × (done : Bool)TodoList := List TodoItemTodoAction ::=| mark_as_done (index : ℕ)| add_task (value : String)initial : TodoList :=[ ("get groceries", false), ("put on instagram", false)]update : TodoList → TodoAction → TodoState| 𝑠 ↦ (mark_as_done 𝑖) ↦ (𝑠 with 𝑠.l[𝑖].done ← true)| 𝑠 ↦ (add_task 𝑣) ↦ (𝑠 with 𝑠.l ← 𝑠.l ++ [(𝑣, false)])view : TodoList → Html TodoActionview l :=<ul>{l.mapi $ (i, label, done) ↦<li>{if done then "[x]" else "[ ]"}{label}{if not done then<button click={() ↦ mark_as_done i}>mark done</button>else []}</li>}<hr/><li> {textbox} </li></ul>
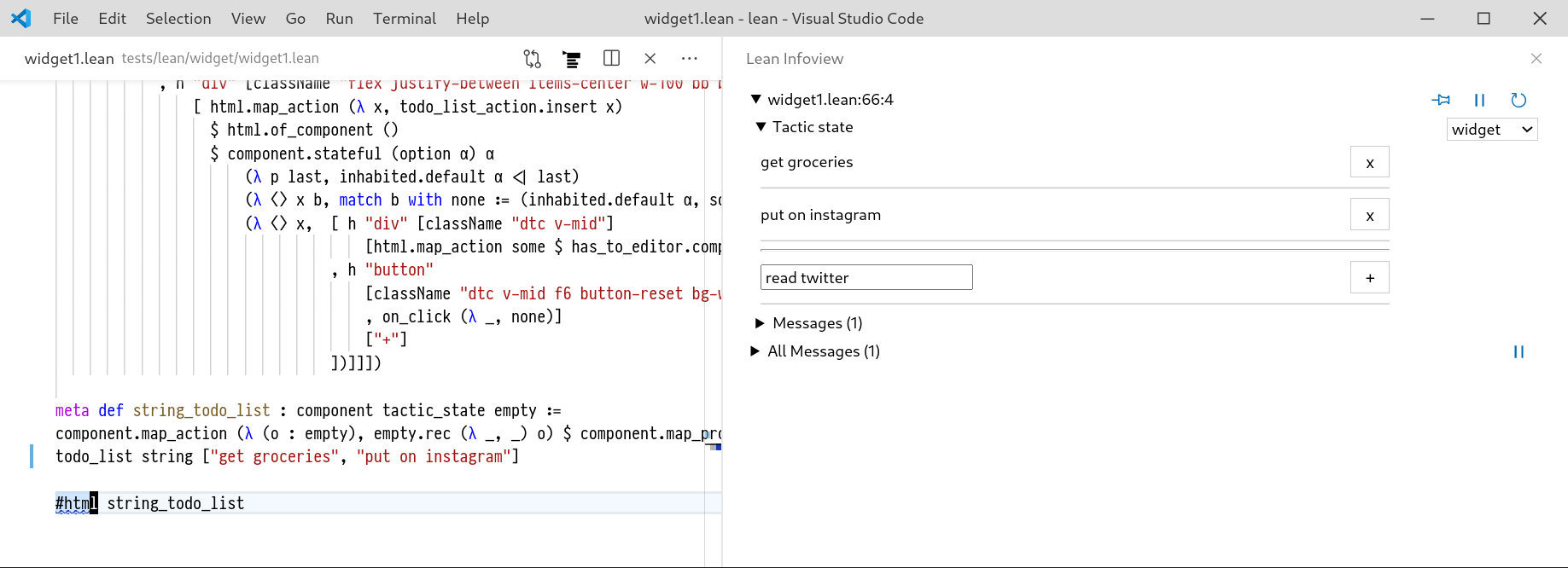
A todo list component implemented in Lean 3 using an inner textbox component, demonstrating state encapsulation. As we type "read twitter" in the textbox, the state of the textbox component is updating but the external component's state does not change.
C.2. Abstracting the Html datatype
So now we have a framework for building apps. However now before explaining how to create a model for a widget, I want to generalise this a little further.
Because really the algorithm for maintaining the view model is more general than with Html and instead is more about trees where events on the trees can cause changes.
This work differs from React, Elm and similar functional UI frameworks in that it generalises the algorithm to an arbitrary tree structure.
So let's generalise Html A to instead be some arbitrary inductive datatype. To do this, note that we can write
HtmlBase A X ::=| element : String → List (Attr A) → List X → HtmlBase A X| of_string : String → HtmlBase A X
And now Html A is the fixpoint of HtmlBase A. That is, Html A = HtmlBase A (Html A).
In this section we will abstract HtmlBase A to an arbitrary 'base functor' Q (E : Type) (X : Type) : Type.
The E type parameter represents the points where event handlers should exist on the tree.
Further, choose some type EventArgs to represent the data that the UI can send back to an event handler as a result of an interaction with the user.
In the todo-list example in the previous section, this was Unit for the click events and String for the textbox change events.
For simplicity let's assume that all of the event args are the same.
So in the case of Html we would choose Q such that Fix (Q (EventArgs → A)) is isomorphic to Html A.
In this section I will assume that Q is traversable on both arguments and has coordinates CPlease refer to Section 2.3.2..
Then our input will be an object UTree:
UTree A :=| mk (v : Q (EventArgs → A) (UTree A))| of_component (c : Component P A) (p : P)Hook Pₒ Aₒ Pᵢ Aᵢ :=(S : Type)× (init : Pₒ → S × Pᵢ)× (reconcile : Pₒ → S → S × Option Pᵢ)× (update : Aᵢ → S → S × Option Pᵢ × Option Aₒ)Component P A ::=| pure (view : P → UTree A)| with_hook (h : Hook P A P' A') (c : Component P' A')
C.3. Holding a general representation of the UI state.
So our goal here is to make a VComponent type that represents the UI state of a given system.
ComponentId := ℕVTree A| mk (v : Q (EventArgs → A) (VTree A))| of_component(id : ComponentId)(c : Component P A)(p : P)(vc : VComponent P A)VComponent P A :=| pure (view : P → UITree A) (render : VTree A)| with_hook (h : Hook P A P' A') (s : h.S) (vc : VComponent P' A')
So here, the UTree is a tree that the programmer creates to specify the behaviour of the widget and the VTree is this tree along with the states produced by each Hook.
To create a VTree from a UTree, we use init:
mutable id_count ← 0init : UTree A → VTree A :=| mk 𝑣 ↦ mk (init <$> 𝑣)| of_component 𝑐 𝑝 ↦ of_component (id_count++) 𝑐 𝑝 (init 𝑐 𝑝)init : Component P A → P → VComponent P A| pure 𝑓 ↦ 𝑝 ↦ pure 𝑓 $ 𝑓 𝑝| with_hook 𝑐 ↦ 𝑝 ↦let (𝑠, 𝑝') := .init 𝑝 in with_hook 𝑠 $ init 𝑐 𝑝'
Where id_count++ returns the current value of id_count and increments it.
A pure functional implementation would avoid this mutability by wrapping everything in a state monad, but I have omitted this in the name of reducing clutter.
C.4. Reconciliation
Once the states are initialised, we need a way of updating a tree. This is the process where we have a 𝑣 : VTree representing the current state of the application and an 𝑢 : UTree representing some new tree that should replace 𝑣. For example 𝑢 might be a tree created for the todo-list app with a new task in the list.
However all of the states on 𝑣 must be 'carried over' to the new tree 𝑢. In our todo-list example, this is the constraint that the text in the new-todo textbox should not be reset if we interact with some other part of the app.
Sticking with the lingo of ReactJS, let's call this reconciliation, however ReactJS reconciliation is a more specialised affair. The purpose of reconciliation is to compare the UI tree from before the change with a new UI tree and to match up any components whose state needs to be preserved. Additionally, it is used as an efficiency measure so that components whose props have not changed do not need to be recomputed.
Q_reconcile(init : Y → X)(rec : X → Y → X)(old : Q E X)(new : Q E Y): Q E Xreconcile: VTree A → UITree A → VTree A| mk 𝑣 ↦ mk 𝑢 ↦mk $ Q_reconcile init reconcile 𝑣 𝑢| of_component 𝑖 𝑐₀ _ 𝑣𝑐 ↦ of_component 𝑐 𝑝 ↦if 𝑐 ≠ 𝑐₀ then init (of_component 𝑐 𝑝)else of_component 𝑖 𝑐 𝑝 (reconcile 𝑣𝑐 𝑐 𝑝)| _ ↦ 𝑡 ↦ init 𝑡reconcile: VComponent P A → P → VComponent P A| pure 𝑓 𝑣 ↦ 𝑝 ↦ pure 𝑓 $ reconcile 𝑣 $ 𝑓 𝑝| with_hook 𝑠 𝑣𝑐 ↦ 𝑝 ↦match .reconcile 𝑝 𝑠 with| (𝑠', none) ↦ with_hook 𝑠' 𝑣𝑐| (𝑠', some 𝑝') ↦ with_hook 𝑠' $ reconcile 𝑣𝑐 𝑝'
Here, Q_reconcile is a function that must be implemented per Q. It should work by comparing old : Q E X and new : Q E Y and then pairing off children of x : X, y : Y of old and new and applying the recursive rec x y to reconcile the children. In the case of children y that can't be paired with a child from the old tree, they should be converted using init y.
For example, in the case of Q being HtmlBase, an algorithm similar to the one given by ReactJS is used.
There is a little fudge in the above code, namely that c ≠ c₀ is not technically decidable: view f = view g would require checking equality on functions f = g.
So the necessary fudge is to instead perform a reference equality check on the components or to demand that each Component is also constructed with some unique identifier for checking.
In the actual Lean implementation, the equality check is performed by comparing the hashes of the VM objects for c and c₀.
Once we have built a VTree representing the current interaction state of the widget, we need to convert this to pixels on the screen.
The first step here is to strip out the components and produce a pure tree representing the UI tree that will be displayed.
For the implementation of ProofWidgets in Lean, the final format to be sent to the client is a JSON object representing the HTML DOM that will then be rendered using React and the web browser.
Suppose that the functor Q _ X has coordinates CE.
This means that we can make get and coords for VTree A, with the type List C × CE.
get : (List C × CE) → VTree X → Option (EventArgs → A)| ([], 𝑒) ↦ mk 𝑣 ↦ get 𝑒 𝑣| ( :: 𝑡, 𝑒) ↦ mk 𝑣 ↦ do𝑢 : VTree X ← get 𝑣,get (𝑡, 𝑒) 𝑢| _ ↦ _ ↦ nonecoords : VTree X → List (List C × CE)| (mk 𝑣 ) ↦for (𝑒 : CE) in coords 𝑣:yield ([], 𝑒)for (𝑐 : C) in coords 𝑣:some (𝑥 : VTree X) ← get 𝑣 𝑐for (𝑙, 𝑒) in coords 𝑥:yield ([𝑐, ..𝑙], 𝑒)
We will use this to attach to each event handler in the VTree a distinct, serialisable address.
This is needed because we will be sending the output tree via JSON to the client program and then if the user clicks on a button or
hovers over some text, we will need to be able to discover which part of the interface they used.
HandlerId := (adr : (List C × CE)) × (route : List ComponentId)OutputTree := Q (HandlerId) (OutputTree)render : List ComponentId → VTree A → OutputTree| 𝑙 ↦ mk 𝑣 ↦𝑢 : Q HandlerId (VTree A) ← traverse_with_coord (𝑎 ↦ ↦ (𝑎, 𝑙)) 𝑣,render 𝑙 <$> 𝑢| 𝑙 ↦ (of_component 𝑖 𝑐 𝑝 𝑣𝑐) ↦ render ([..𝑙, 𝑖]) 𝑣𝑐render : List ComponentId → VComponent P A → OutputTree| 𝑙 ↦ pure 𝑣 𝑟 ↦ render 𝑙 𝑟| 𝑙 ↦ with_hook 𝑠 𝑣𝑐 ↦ render 𝑙 𝑣𝑐
Now that the output tree is generated, we can send it off to the client for turning in to pixels.
Then the system need only wait for the user to interact with it.
When the user does interact, the client will find out through the browser's API, and this will in turn be used to track down the HandlerId that was assigned for this event.
The client will then send a widget_event payload back to the ProofWidgets engine consisting of 𝑒: EventArgs and a handler 𝑖 : HandlerId .
The handle_event routine takes 𝑒 and 𝑖 and updates the VDOM object by finding the event handler addressed by 𝑖, running the event handler and then propagating the resulting action back up to the root node of the tree.
handle_event (𝑒 : EventArgs) (𝑖 : HandlerId): VComponent P A → (Option A) × (VComponent P A)| pure 𝑓 𝑣 ↦ let (𝑎, 𝑣) := handle_event 𝑒 𝑖 𝑣 in (𝑎, pure 𝑣)| with_hook 𝑠 𝑣 ↦let (𝑏, 𝑣) := handle_event 𝑒 𝑖 𝑣 inmatch b with| none := (none, with_hook 𝑠 𝑣)| (some 𝑏) :=match .update 𝑏 𝑠 with| (𝑠, none , 𝑎) := (𝑎, with_hook 𝑠 𝑣)| (𝑠, some 𝑝, 𝑎) := (𝑎, with_hook 𝑠 $ reconcile 𝑣 𝑝)handle_event (𝑒 : EventArgs): HandlerId → VTree A → (Option A) × VTree A| (𝑙, []) ↦ mk 𝑣 ↦(some ) ← get 𝑙 𝑣handle_action ( 𝑒)| (𝑙, [𝑖, ..𝑟]) ↦ 𝑣 ↦for 𝑥 in get_component_coords 𝑣:some (of_component 𝑖 𝑐 𝑝 𝑣𝑐) ← get 𝑐𝑜 𝑣(𝑜𝑎, 𝑣𝑐) ← handle_event 𝑒 (𝑙, 𝑟) 𝑣𝑐return (𝑜𝑎, set 𝑥 𝑣 $ of_component 𝑖 𝑐 𝑝 𝑣𝑐)| _ ↦ _ ↦ throw "event handler not found"
This completes the definition of the core abstract widget loop.
Lemma C.14: The above recursive definitions are all well-founded. And so the reconciliation algorithm will not loop indefinitely.
Proof: By inspecting the structure of the above recursive function definitions. One can verify that at each recursive call, the size of the UTree, VTree, Component and VComponent instances being recursed over is strictly decreasing.
This means that the algorithm will terminate by a routine application of well-founded recursion. I have confirmed this by implementing a simplified version of the presented algorithm in Lean 3 and making use of Lean's automation on checking the well-foundedness of recursive functions.
C.5. Implementation
The implementation of these algorithms is in C++, and the Lean-facing API is decorated with the meta keyword to indicate that it is untrusted by the kernel.
The actual API for ProofWidgets in the Lean 3 theorem prover needs to be untrusted because:
It is convenient to allow HTML attributes to take values in untrusted datatypes such as
float.The C++ implementation needs to handle additional component types not mentioned in the previous subsection such as effects.
Inductive type declarations in Lean do not have good support for having lists of recursive arguments (eg
inductive T | mk : (list T) → T), but it makes most sense to implement the API with lists to match the XML document model.The only consumer of the ProofWidgets API is the Lean source, so we don't lose much by not trusting the definitions.
init, reconcile and handle_event terminate by inspection since the each recursive call acts on a strictly smaller subtree.
Suppose that the user triggers two events in rapid succession, it might be the case that the second event is triggered before the UI has updated, and so the HandlerId of the second event refers to the old VTree which may have been updated.
If the latency of the connection between client and server is low, then this is not much of an issue. However it may become apparent when using ProofWidgets remotely such as with VSCode's develop-over-SSH feature. Or if ProofWidget's rendering methods rely on a long-running task such as running some proof automation. In these cases the UI may become unresponsive or behave in unexpected ways.
There are two approaches to dealing with this:
Simply throw away all of these queued events. However this generally leads to unresponsive UI, particularly for mouse movement driven events such as hovering over subterms.
Attempt to call
handle_eventwith the out-of-dateHandlerIdanyway. This makes the app more responsive, because multiple events can be queued duringhandle_eventinstead of dropped. If the second event' sHandlerIdis no longer a valid address for theVTree, then it will harmlessly error and be ignored. The difficult case is when theHandlerId's address is valid but points to a different handler than the one rendered in the DOM. For example, there could be a pair of buttons, and clicking the first button swaps the order of the buttons. If the user clicks this button rapidly, then the second click will apply to the swapped button instead of the same button twice.
Currently, the Lean 3 implementation uses the first approach in this list, however this can cause unresponsiveness if a long-running tactic is used in the rendering method. As noted in Section 5.9, I intend to overcome this by adding a task-based system to components (5.19) rather than fix the event model.
Bibliography for this chapter
- [Ell01]Elliott, ConalFunctional Image Synthesis (2001)Proceedings of Bridgeshttp://conal.net/papers/bridges2001/