Now that we have reviewed the requisite background material, I can define the moving parts of a human-like theorem prover. The driving principle is to find ways of representing proofs at the same level of detail that a human mathematician would use to communicate to colleagues.

The contributions of this chapter are:

• The Box datastructure, a development calculus (Section 3.3) designed to better capture how humans reason about proofs while also being formally sound.

• A set of inference rules on Box which preserve this soundness (Section 3.5).

• A natural language write-up component converting proof objects created with this layer to an interactive piece of text (Section 3.6).

• In the supplementary Appendix A, an 'escape hatch' from the Box datastructure to a metavariable-oriented goal state system as used by Lean (Section 3.4.4, Appendix A). This enables compatibility between Box-style proofs and existing automation and verification within Lean.

HumanProof integrates with an existing proof assistant (in this case Lean). By plugging in to an existing prover, it is possible to gain leverage by utilising the already developed infrastructure for that prover such as parsers, tactics and automation. Using an existing prover also means that the verification of proofs can be outsourced to the prover's kernel.

The first research question of Section 1.2 was to investigate what it means for a proof to be human-like. I provided a review to answer this question in Section 2.6. Humans think differently to each other, and I do not wish to state that there is a 'right' way to perform mathematics. However, I argue that there are certain ways in which the current methods for performing ITP should be closer to the general cluster of ways in which humans talk about and solve problems.

In this chapter I investigate some ways in which the inference rules that provers use could be made more human-like, and then introduce a new proving abstraction layer, HumanProof, written in the Lean 3 theorem prover, implementing these ideas. Later, in Chapter 6, I gather thoughts and ratings from real mathematicians about the extent to which the developed system achieves these goals.

In Section 3.1, I first present an example proof produced by a human to highlight the key features of 'human-like' reasoning that I wish to emulate. Then in Section 3.2 I give an overview of the resulting designs and underline the primary design decisions and the evidence that drives them. In Section 3.3 I provide the details and theory of how the system works through defining the key Box structure and tactics on Boxes. The theory behind creating valid proof terms from Boxes is presented in Section 3.4 as well as how to run standard tactics within Boxes (Section 3.4.4). This theoretical basis will then be used to define the human-like tactics in Section 3.5. Then, I will detail the natural language generation pipeline for HumanProof in Section 3.6.

3.1. Motivation

Building on the background where I explored the literature on the definition of 'human-like' (Section 2.6) and 'understandable' (Section 2.5.1) proofs, my goal in this section is find some specific improvements to the way in which computer aided mathematics is done. I use these improvements to motivate the design choices of the HumanProof system.

3.1.1. The need for human-like systems

In Section 1.1, I noted that non-specialist mathematicians have yet to widely accept proof assistants despite the adoption of other tools such as computer algebra systems. Section 1.1 presented three problems that mathematicians have with theorem provers: differing attitudes on correctness, a high learning cost to learning to use ITP and a low resulting reward -- learning the truth of something that they 'knew' was true anyway. One way in which to improve this situation is to reduce the cost of learning to use proof assistants through making the way in which they process proofs more similar to how a human would process proofs, making the proofs more closely match what the mathematician already knows. Making a prover which mimics a human's thought process also helps overcome the problem of differing attitudes of correctness.

Requiring a human-like approach to reasoning means that many automated reasoning methods such as SMT-solvers and resolution (see Section 2.6) must be ruled out. In these machine-oriented methods, the original statement of the proposition to be proved is first reduced to a normal form and mechanically manipulated with a small set of inference rules. The resulting proof is scarcely recognisable to a mathematician as a proof of the proposition, even if it is accepted by the kernel of a proof assistant. As discussed in Section 1.1, Section 2.5 and as will be confirmed in Chapter 6, mathematicians do not care just about a certificate that a statement is correct but also about the way in which the statement is correct.

Given some new way of creating proofs; how can we determine whether these created proofs are more 'human-like' than some other system? The way I propose here is to require that the program be able to imitate the reasoning of humans at least well enough to produce convincing natural language write-ups of the proofs that it generates, and then to test how convincing these write-ups are through asking mathematicians. This approach is shared by the previous work of Gowers and Ganesalingam [GG17[GG17]Ganesalingam, Mohan; Gowers, W. T.A fully automatic theorem prover with human-style output (2017)Journal of Automated Reasoninghttps://doi.org/10.1007/s10817-016-9377-1] Gowers and Ganesalingam is abbreviated G&G., where they use a similar framework to the HumanProof system presented in this thesis to produce natural language write-ups of proofs for some lemmas in the domain of metric space topology. The work presented in this thesis builds significantly on the work of G&G.

3.1.2. Modelling human-like reasoning

One of the key insights of Gowers and Ganesalingam is that humans reason with a different 'basis' of methods than the logical operations and tactics that are provided to the user of an ITP. For example, a hypothesis such as a function $f:X\to Y$ being continuous expands to a formula (3.1) with interlaced quantifiers.

However in a mathematical text, if one needs to prove $\mathbf{d}(f(x),f(y))<\epsilon$, the hypothesis that $f$ is continuous will be applied in one go. That is, a step involving (3.1) would be written as "Since $f$ is continuous, there exists a $\delta >0$ such that $\mathbf{d}(f(x),f(y))<\epsilon$ whenever $\mathbf{d}(x,y)<\delta$". Whereas in an ITP this process will need to be separated in to several steps: first show $x\in X$, then obtain $\delta$, then show $\mathbf{d}(x,y)<\delta$.

Another example with the opposite problem is the automated tactics such as the tableaux prover blast [Pau99[Pau99]Paulson, Lawrence CA generic tableau prover and its integration with Isabelle (1999)Journal of Universal Computer Sciencehttps://doi.org/10.3217/jucs-005-03-0073]. The issue with tactics is that their process is opaque and leaves little explanation for why they succeed or fail. They may also step over multiple stages that a human would rather see spelled out in full. The most common occurrence of this is in definition expansion; two terms may be identical modulo definition expansion but a proof found in a textbook will often take the time to point out when such an expansion takes place.

This points towards creating a new set of inference rules for constructing proofs that are better suited for creating proofs by corresponding better to a particular reasoning step as might be used by a human mathematician.

3.1.3. Structural sharing

Structural sharing is defined as making use of the same substructure multiple times in a larger structure. For example, a tree with two branches being the same would be using structural sharing if the sub-branches used the same object in memory. Structural sharing of this form is used frequently in immutable datastructures for efficiency. However here I am interested in whether structural sharing has any applications in human-like reasoning.

When humans reason about mathematical proofs, they often flip between forwards reasoning and backwards reasoningBroadly speaking, forwards reasoning is any mode of modifying the goal state that acts only on the hypotheses of the proof state. Whereas backwards reasoning modifies the goals.. The goal-centric proof state used by ITPs can make this kind of reasoning difficult. In the most simple example, suppose that the goal is P ∧ Q ⊢ Q ∧ PThat is, given the hypothesis P ∧ Q, prove Q ∧ P where P and Q are propositions and ∧ is the logical-and operation.. One solution is to perform a split on the goal to produce P ∧ Q ⊢ Q and P ∧ Q ⊢ P. However, performing a conjunction elimination on the P ∧ Q hypothesis will then need to be performed on both of the new goals. This is avoided if the elimination is performed before splitting P ∧ Q. In this simplified example it is clear which order the forwards and backwards reasoning should be performed. But in more complex proofs, it may be difficult to see ahead how to proceed. A series of backwards reasoning steps may provide a clue as to how forwards reasoning should be applied. The usual way that this problem is solved is for the human to edit an earlier part of the proof script with the forwards reasoning step on discovering this. I reject this solution because it means that the resulting proof script no longer represents the reasoning process of the creator. The fact that the forwards reasoning step was motivated by the goal state at a later point is lost.

The need to share structure among objects in the name of efficiency has been studied at least as far back as Boyer and Moore [BM72[BM72]Boyer, R. S.; Moore, J. S.The sharing structure in theorem-proving programs (1972)Machine intelligencehttps://www.cs.utexas.edu/~moore/publications/structure-sharing-mi7.pdf]. However, the motivation behind introducing it here is purely for the purpose of creating human-like proofs.

The solution that I propose here is to use a different representation of the goal state that allows for structural sharing. This alteration puts the proof state calculus more in the camp of OLEG [McB00[McB00]McBride, ConorDependently typed functional programs and their proofs (2000)PhD thesis (University of Edinburgh)http://hdl.handle.net/1842/374], and the G&G prover. The details of the implementation of structural sharing are presented later in Section 3.5.4.

Structural sharing can also be used to implement backtracking and counterfactuals. For example, suppose that we need to prove A ⊢ P ∨ Q, one could apply the ∨-left-introduction rule P ⇒ P ∨ Q, but then one might need to backtrack later in the event that really the right-introduction rule Q ⇒ P ∨ Q should be used instead. Structural sharing lets us split a goal into two counterfactuals.

3.1.4. Verification

One of the key benefits of proof assistants is that they can rigorously check whether a proof is correct. This distinguishes the HumanProof project from the prior work of G&G, where no formal proof checking was present. While I have argued in Section 2.5 (and will later be suggested from the results of my user study in Section 6.6) that this guarantee of correctness is less important for attracting working mathematicians, there need not be a conflict between having a prover which is easy for non-specialists to understand and which is formally verified.

3.1.5. What about proof planning?

Proof planning is the process of creating proofs using abstract proof methods that are assembled with the use of classical AI planning algorithms[RN10]Russell, Stuart J.; Norvig, PeterArtificial Intelligence - A Modern Approach (2010)publisher Pearson Educationhttp://aima.cs.berkeley.edu/An introduction to classical AI planning can be found in Russel and Norvig [RN10 Pt.III].. The concept of proof planning was first introduced by Bundy [Bun88[Bun88]Bundy, AlanThe use of explicit plans to guide inductive proofs (1988)International conference on automated deductionhttps://doi.org/10.1007/BFb0012826]. A review of proof planning is given in Section 2.6.2. The advantage of proof planning is that it represents the way in which a problem will be solved at a much more abstract level, more like human mathematicians.

The primary issue with proof planning is that there is a sharp learning curve. In order to get started with proof plans, one must learn a great deal of terminology and a new way of thinking about formalised mathematics. The user has to familiarise themselves with the way in which proof methods are used to construct proof plans and how to diagnose malformed plans for their particular problems. Bundy presents his own critique of proof planning [Bun02[Bun02]Bundy, AlanA critique of proof planning (2002)Computational Logic: Logic Programming and Beyondhttps://doi.org/10.1007/3-540-45632-5_7] which goes in to more detail on this point.

The study of proof planning has fallen out of favour for the 21st century so far, possibly in relation to the rise of practical SMT solvers such as E prover [SCV19[SCV19]Schulz, Stephan; Cruanes, Simon; Vukmirović, PetarFaster, Higher, Stronger: E 2.3 (2019)Proc. of the 27th CADE, Natal, Brasilhttp://wwwlehre.dhbw-stuttgart.de/~sschulz/bibliography.html#SCV:CADE-2019] and Z3 prover [MB08[MB08]de Moura, Leonardo; Bjørner, NikolajZ3: An efficient SMT solver (2008)International conference on Tools and Algorithms for the Construction and Analysis of Systemshttps://doi.org/10.1007/978-3-540-78800-3_24] and their incorporation in to ITP through the use of 'hammer' software like Isabelle's Sledgehammer [BN10[BN10]Böhme, Sascha; Nipkow, TobiasSledgehammer: judgement day (2010)International Joint Conference on Automated Reasoninghttps://doi.org/10.1007/978-3-642-14203-1_9]. I share a great deal of the ideals that directed proof planning and the equational reasoning system presented in Chapter 4 is inspired by it. I take a more practical stance; the additional abstractions that are placed atop the underlying tactic system should be transparent, in that they are understandable without needing to be familiar with proof planning and with easy 'escape hatches' back to the tactic world if needed. This design goal is similar to that of the X-Barnacle prover interface [LD97[LD97]Lowe, Helen; Duncan, DavidXBarnacle: Making Theorem Provers More Accessible (1997)14th International Conference on Automated Deductionhttps://doi.org/10.1007/3-540-63104-6_39] (discussed later in Section 5.1), where a GUI is used to present an explorable representation of a proof plan.

3.2. Overview of the software

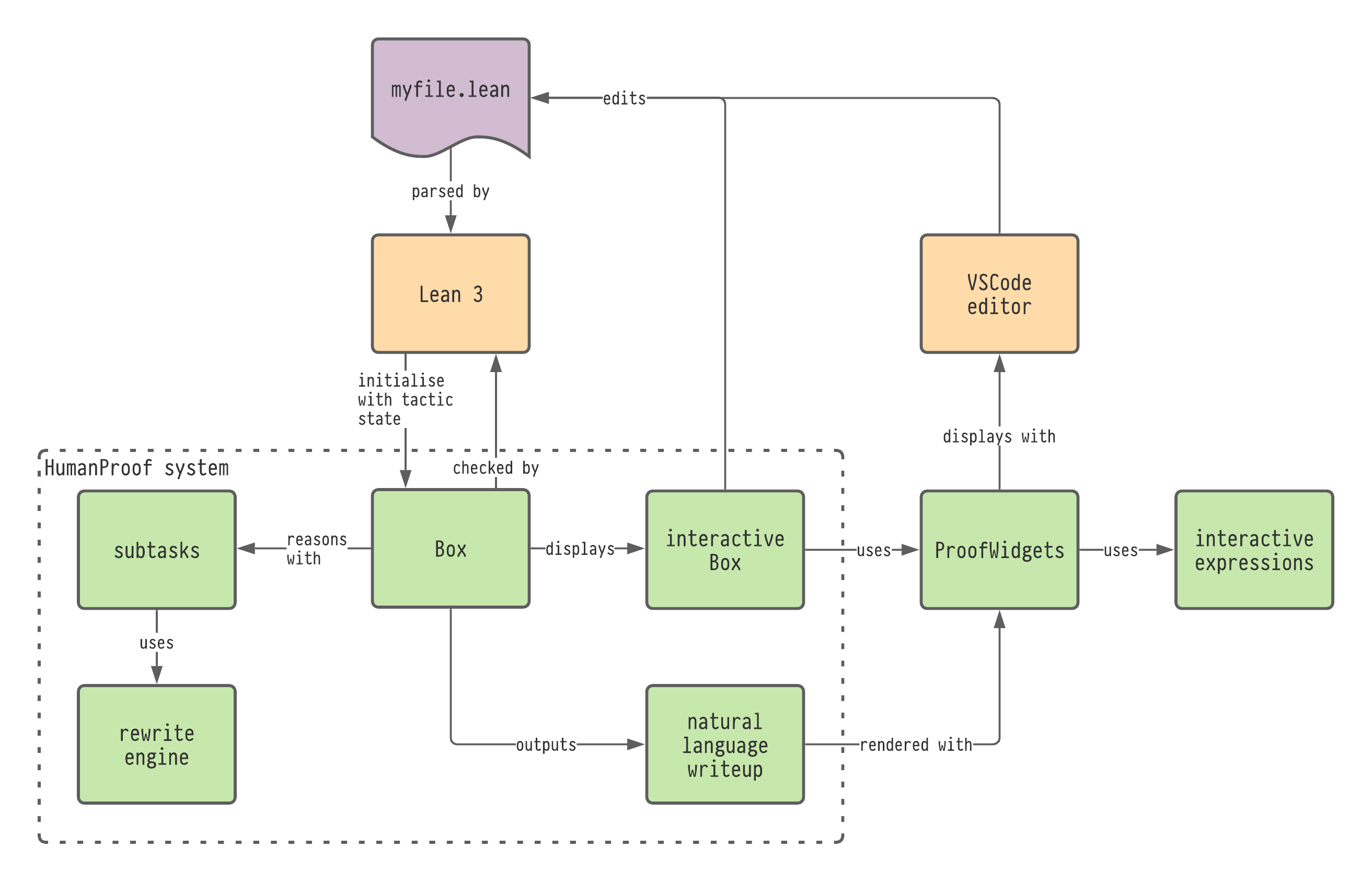
The software implementation of the work presented in this thesis is called 'HumanProof' and is implemented using the Lean 3 prover. The source code can be found at https://github.com/edayers/lean-humanproof-thesis. In this section I give a high-level overview of the system and some example screenshots. A general overview of the system and how it relates to the underlying Lean theorem prover is shown in Figure 3.2.

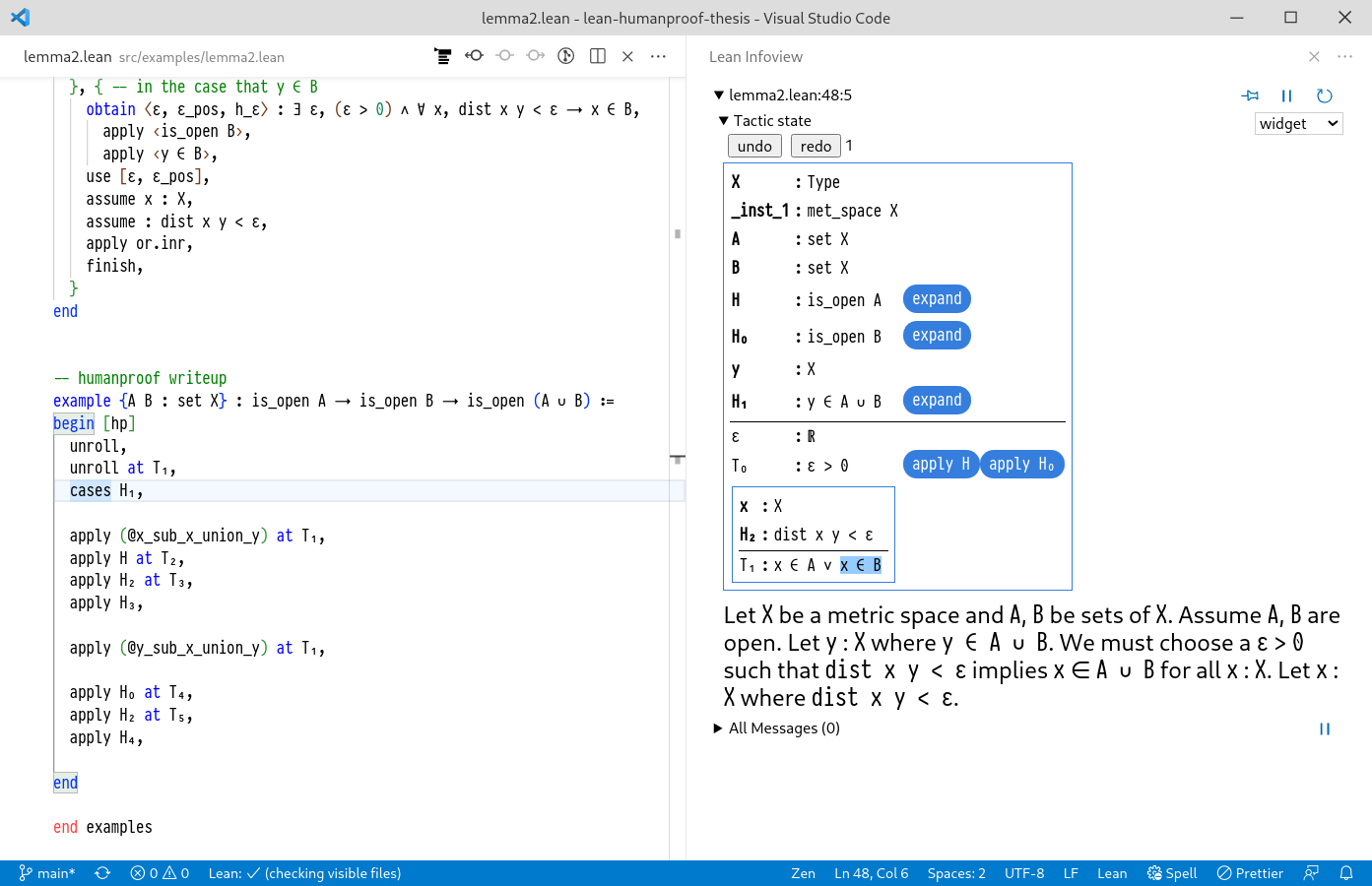
Given a theorem to prove, HumanProof is invoked by indicating a special begin [hp] script block in the proof document (see Figure 3.3). This initialises HumanProof's Box datastructure with the assumptions and goal proposition of the proof. The initial state of the prover is shown in the goal view of the development environment, called the Info View (the right panel of Figure 3.3). Using the ProofWidgets framework (developed in Chapter 5), this display of the state is interactive: the user can click at various points in the document to determine their next steps. Users can then manipulate this datastructure either through the use of interactive buttons or by typing commands in to the proof script in the editor. In the event of clicking the buttons, the commands are immediately added to the proof script sourcefile as if the user had typed it themselves (the left panel of Figure 3.3). In this way, the user can create proofs interactively whilst still preserving the plaintext proof document as the single-source-of-truth; this ensures that there is no hidden state in the interactive view that is needed for the Lean to reconstruct a proof of the statement. While the proof is being created, the system also produces a natural language write-up (labelled 'natural language writeup' in Figure 3.2) of the proof (Section 3.6) that is displayed alongside the proof state. As the proof progresses, users can see the incomplete natural language proof get longer too.

The system also comes equipped with a module for solving equalities using the 'subtasks algorithm' (Chapter 4); labelled 'subtasks' on Figure 3.2. The subtasks algorithm uses a hierarchical planning (see Section 2.6.2) system to produce an equality proof that is intended to match the way that a human would create the proof, as opposed to a more machine like approach such as E-matching [BN98[BN98]Baader, Franz; Nipkow, TobiasTerm rewriting and all that (1998)publisher Cambridge University Presshttps://doi.org/10.1017/CBO9781139172752 Ch. 10]. The output of this subsystem is a chain of equations that is inserted into the natural language writeup.

3.3. The Box datastructure

At the heart of HumanProof is a development calculus using a datastructure called Box. The considerations from Section 3.1.3 led to the development of an 'on-tree' development calculus. Rather than storing a flat list of goals and a metavariable context alongside the result, the entire development state is stored in a recursive tree structure which I call a Box. The box tree, to be defined in Section 3.3.2, stores the proof state as an incomplete proof tree with on-tree metavariable declarations which is then presented to the user as a nested set of boxes.

3.3.1. An example of Box in action.

Before defining boxes in Section 3.3.2, let's look at a simple example. Boxes are visualised as a tree of natural-deduction-style goal states. Let's start with a minimal example to get a feel for the general progression of a proof with the Box architecture. Let's prove P ∨ Q → Q ∨ P using Boxes. The initial box takes the form (3.4).

And we can read (3.4) as saying "we need to show P ∨ Q → Q ∨ P". The ?𝑡 is the name of the metavariable that the proof of this will be assigned to. The first action is to perform an intro step to get (3.5).

To be read as "Given P ∧ Q, we need to show Q ∨ P". So far the structure is the same as would be observed on a flat goal list structure. The idea is that everything above a horizontal line is a hypothesis (something that we have) and everything below is a goal (something we want). When all of the goals are solved, we should have a valid proof of the original goal. At this point, we would typically perform an elimination step on ℎ (e.g., cases ℎ in Lean) (3.6).

Here in (3.6) we can see nested boxes, each nested box below the horizontal line must be solved to solve the parent box. However, in the box architecture there is an additional step available; a branching on the goal (3.7).

If a pair of boxes appear with a ⋁ between them, then either of the boxes can be solved to solve the parent box. And then we can eliminate h on the branched box:

Now at this point, we can directly match 𝑕₁ with ?𝑡₁₂ and 𝑕₂ with ?𝑡₂₁ to solve the box. Behind the scenes, the box is also producing a result proof term that can be checked by the proof assistant's kernel.

3.3.2. Definition of Box

The above formulation is intended to match with the architecture designed in G&G, so that all of the same proof-steps developed in G&G are available. Unlike G&G, the system also interfaces with a flat goal-based development calculus, and so it is possible to use both G&G proof-steps and Lean tactics within the same development calculus. To do this, let's formalise the system presented above in Section 3.3.1 with the following Box datatype (3.9). Define a Binder := (name : Name) × (type : Expr) to be a name identifier and a type with notation (name∶type), using a smaller colon to keep the distinction from a meta-level type annotation.

Box ::=
| ℐ (x : Binder) (b : Box) : Box
| 𝒢 (m : Binder) (b : Box) : Box
| 𝒭 (r : Expr) : Box
| 𝒜 (b₁ : Box) (r : Binder) (b₂ : Box) : Box
| 𝒪 (b₁ : Box) (b₂ : Box) : Box
| 𝒱 (x : Binder) (t : Expr) (b : Box) : Box

I will represent instances of the Box type with a 2D box notation defined in (3.10) to make the connotations of the datastructure more apparent.

These visualisations are also presented directly to the user through the use of the widgets UI framework presented in Chapter 5. The details of this visualisation are given in Section 5.8.

To summarise the roles for each constructor:

• ℐ 𝑥 𝑏 is a variable introduction binder, that is, it does the same job as a lambda binder for expressions and is used to introduce new hypotheses and variables.

• 𝒢 𝑚 𝑏 is a goal binder, it introduces a new metavariable ?𝑚 that the child box depends on.

• 𝒭 𝑟 is the result box, it depends on all of the variables and goals that are declared above it. It represents the proof term that is returned once all of the goal metavariables are solved. Extracting a proof term from a well-formed box will be discussed in Section 3.4.

• 𝒜 𝑏₁ (𝑥 ∶ α) 𝑏₂ is a conjunctive pair of boxes. Both boxes have to be solved to complete the proof. Box b₂ depends on variable 𝑥. When 𝑏₁ is solved, the 𝑥 value will be replaced with the resulting proof term of 𝑏₁.

• 𝒪 𝑏₁ 𝑏₂ is a disjunctive pair, if either of the child boxes are solved, then so is the total box. This is used to implement branching and backtracking.

• 𝒱 𝑥 𝑏 is a value binder. It introduces a new assigned variable.

Boxes also have a set of well-formed conditions designed to follow the typing judgements of the underlying proof-assistant development calculus. This will be developed in Section 3.4.

3.3.3. Initialising and terminating a Box

Given an expression representing a theorem statement P : Expr, ∅ ⊢ P ∶ Prop, we can initialise a box to solve P as 𝑏₀ := 𝒢 (𝑡 ∶ P) (𝒭 𝑡) (3.11).

In the case that P also depends on a context of hypotheses Γ ⊢ P ∶ Prop, these can be incorporated by prepending to the initial 𝑏₀ in (3.11) with an ℐ box for each 𝑕 ∈ Γ. For example, if Γ = [(𝑥∶α), (𝑦∶β)] then send 𝑏₀ to ℐ (𝑥∶α), ℐ (𝑦∶β), 𝑏₀.

Say that a Box is solved when there are no 𝒢-binders remaining in the Box. At this point, the proving process ceases and a proof term and natural language proof may be generated.

3.3.4. Transforming a Box

The aim is to solve a box through the use of a sequence of sound transformations on it. Define a box-tactic is a partial function on boxes BoxTactic := Box → Option Box. Box-tactics act on Boxes in the same way that tactics act on proof states. That is, they are functions which act on a proof-state (i.e., a representation of an incomplete proof) in order to prove a theorem. This is to make it easier to describe how box-tactics interface with tactics in Section 3.4 and Appendix A.

In Section 3.3.1 we saw some examples of box-tactics to advance the box state and eventually complete it. A complete set of box-tactics that are implemented in the system will be given in Section 3.5.

As with tacticsAt least, tactics in a 'checker' style proof assistant such as Lean. See Section 2.1 for more information., there is no guarantee that a particular box-tactic will produce a sound reasoning step; some box-tactics will be nonsense (for example, a box-tactic that simply deletes a goal) and not produce sound proofs. In Section 3.4 I will define what it means for a box-tactic to be sound and produce a correct proof that can be checked by the ITP's kernel.

3.3.5. Relation to other development calculi

Thee Box calculus's design is most similar to McBride's OLEG [McB00[McB00]McBride, ConorDependently typed functional programs and their proofs (2000)PhD thesis (University of Edinburgh)http://hdl.handle.net/1842/374] and G&G's prover [GG17[GG17]Ganesalingam, Mohan; Gowers, W. T.A fully automatic theorem prover with human-style output (2017)Journal of Automated Reasoninghttps://doi.org/10.1007/s10817-016-9377-1]. A more abstract treatment can be found in the work of Sterling and Harper [SH17[SH17]Sterling, Jonathan; Harper, RobertAlgebraic Foundations of Proof Refinement (2017)CoRRhttp://arxiv.org/abs/1703.05215], implemented within the RedPRL theorem prover.

The novel contribution of the Box calculus developed here is that it works within a Spiwack-style [Spi11[Spi11]Spiwack, ArnaudVerified computing in homological algebra, a journey exploring the power and limits of dependent type theory (2011)PhD thesis (INRIA)https://pastel.archives-ouvertes.fr/pastel-00605836/document]See Section 2.4 for more background information. flat metavariable context model as is used in Lean. That is, it is a layer atop the existing metavariable context system detailed in Section 2.4.3. This means that it is possible for the new calculus to work alongside an existing prover, rather than having to develop an entirely new one as was required for OLEG and the G&G prover. This choice opens many possibilities: now one can leverage many of the advanced features that Lean offers such as a full-fledged modern editor and metaprogramming toolchain [EUR+17[EUR+17]Ebner, Gabriel; Ullrich, Sebastian; Roesch, Jared; et al.A metaprogramming framework for formal verification (2017)Proceedings of the ACM on Programming Languageshttps://doi.org/10.1145/3110278]. This approach also reduces some of the burden of correctness pressed upon alternative theorem provers, because we can outsource correctness checking to the Lean kernel. Even with this protection, it is still frustrating when a development calculus produces an incorrect proof and so I will also provide some theoretical results in Section 3.4 and Appendix A on conditions that must be met for a proof step to be sound. The design of the Box calculus is independent of any particular features of Lean, and so a variant of it may be implemented in other systems.

The central datatype is the Box. This performs the role of holding a partially constructed proof object and a representation of the goals that remain to be solved. As discussed in Section 3.1.3, the purpose is to have a structurally shared tree of goals and assumptions that is also compatible with Lean tactics.

McBride's OLEG [McB00[McB00]McBride, ConorDependently typed functional programs and their proofs (2000)PhD thesis (University of Edinburgh)http://hdl.handle.net/1842/374] is the most similar to the design presented here. OLEG 'holes' are functionally the same as metavariables. That is, they are specially tagged variables that will eventually be assigned with expressions. OLEG provides an additional constructor for expressions called 'hole-bindings' or '$?$-bindings'. Because OLEG is a ground-up implementation of a new theorem prover, hole-bindings can be added directly as constructors for expressions. This is not available in Lean (without reimplementing Lean expressions and all of the algorithms)It might be possible to use Lean's expression macro system to implement hole-bindings, but doing so would still require reimplementing a large number of type-context-centric algorithms such as unification [SB01].[SB01]Snyder, Wayne; Baader, FranzUnification theory (2001)Handbook of automated reasoninghttp://lat.inf.tu-dresden.de/research/papers/2001/BaaderSnyderHandbook.ps.gz. These hole-bindings perform the same role as the 𝒢 constructor in that they provide the context of variables that the hole/metavariable is allowed to depend on. But if the only purpose of a hole-binding is to give a context, then why not just explicitly name that context as is done in other theorem provers? The Box architecture given above is intended to give the best of both worlds, in that you still get a shared goal-tree structure without needing to explicitly bind metavariables within the expression tree. Instead they are bound in a structure on top of it.

Lean and Coq's proof construction systems make use of the metavariable context approach outlined in Section 2.4. The metavariable context here performs the same role as the 𝒢 goal boxes, however this set of goals is flattened in to a list structure rather than stored in a tree as in Box. This makes many aspects such as unification easier but means that structural sharing (Section 3.1.3) is lost. In Section 3.4.4 I show that we do not have to forgo use of the algorithms implemented for a flat metavariable structure to use Boxes.

In Isabelle, proofs are constructed through manipulating the proof state directly through an LCF-style [Mil72[Mil72]Milner, RobinLogic for computable functions description of a machine implementation (1972)Technical Reporthttps://apps.dtic.mil/dtic/tr/fulltext/u2/785072.pdf] kernel of available functionsAs can be seen in the source https://isabelle-dev.sketis.net/source/isabelle/browse/default/src/Pure/thm.ML.. Schematic variables are used to create partially constructed terms.

Sterling and Harper [SH17[SH17]Sterling, Jonathan; Harper, RobertAlgebraic Foundations of Proof Refinement (2017)CoRRhttp://arxiv.org/abs/1703.05215] provide a category-theoretical theory of partially constructed proofs and use these principles in the implementation of RedPRL. They are motivated by the need to create a principled way performing refinement of proofs in a dependently-typed foundation. They develop a judgement-independent framework for describing development calculi within a category-theoretical setting.

Another hierarchical proof system is HiProof [ADL10[ADL10]Aspinall, David; Denney, Ewen; Lüth, ChristophTactics for hierarchical proof (2010)Mathematics in Computer Sciencehttps://doi.org/10.1007/s11786-010-0025-6]. HiProof makes use of a tree to write proofs. The nodes of a tree are invocations of inference rules and axioms and an edge denotes the flow of evidence in the proof. These nodes may be grouped to provide varying levels of detail. These hierarchies are used to describe a proof, whereas a Box here describes a partially completed proof and a specification of hypotheses and goals that must be set to construct the proof.

3.4. Creating valid proof terms from a Box

Note that because we are using a trusted kernel, the result of producing an invalid proof with Box is a mere inconvenience because the kernel will simply reject it. However, in order for the Box structure defined in Section 3.3.2 to be useful within a proof assistant such as Lean as motivated by Section 3.1.4, it is important to make sure that a solved Box produces a valid proof for the underlying trusted kernel. To do this, I will define a typing judgement 𝑀;Γ ⊢ 𝑏 ∶ α and then present a method for extracting a proof term 𝑀;Γ ⊢ 𝑟 ∶ α from 𝑏 with the same type provided 𝑏 is solved.

3.4.1. Assignability for Box

In Section 2.4.2, I introduced the concept of an assignable datastructure for generalising variable-manipulation operations to datatypes other than expressions. We can equip a datatype containing expressions with an assignability structure assign (3.12). This is a variable-context-aware traversal over the expressions present for the datatype. For Box, this traversal amounts to traversing the expressions in each box, while adding to the local context if the subtree is below a binder. The definition of assign induces a definition of variable substitution and abstraction over Boxes.

assign (𝑓 : Context → Expr → M Expr) (Γ : Context)
  : Box       → M Box
  | ℐ 𝑥 𝑏     ↦ pure ℐ <*> assign 𝑓 Γ 𝑥  <*> assign 𝑓 [..Γ, 𝑥] 𝑏
  | 𝒢 𝑚 𝑏     ↦ pure 𝒢 <*> assign 𝑓 Γ 𝑚  <*> assign 𝑓 [..Γ, 𝑚] 𝑏
  | 𝒭 𝑟       ↦ pure 𝒭 <*> assign 𝑓 Γ 𝑟
  | 𝒜 𝑏₁ 𝑥 𝑏₂ ↦ pure 𝒜 <*> assign 𝑓 Γ 𝑏₁ <*> assign 𝑓 Γ 𝑥 <*> assign 𝑓 [..Γ, 𝑥] 𝑏₂
  | 𝒪 𝑏₁ 𝑏₂   ↦ pure 𝒪 <*> assign 𝑓 Γ 𝑏₁ <*> assign 𝑓 Γ 𝑏₂
  | 𝒱 𝑥 𝑡 𝑏   ↦ pure 𝒱 <*> assign 𝑓 Γ 𝑥  <*> assign 𝑓 Γ 𝑡 <*> assign 𝑓 [..Γ, 𝑥≔𝑡] 𝑏

3.4.2. Typing judgements for Box

In Section 2.4, I defined contexts Γ, metavariable contexts 𝑀. As covered in Carneiro's thesis [Car19[Car19]Carneiro, MarioLean's Type Theory (2019)Masters' thesis (Carnegie Mellon University)https://github.com/digama0/lean-type-theory/releases/download/v1.0/main.pdf], Lean's type theory affords a set of inference rules on typing judgements Γ ⊢ 𝑡 ∶ α, stating that the expression 𝑡 has the type α in the context Γ. However, these inference rules are only defined for expressions 𝑡 : Expr that do not contain metavariables. In Appendix A.1, I extend these judgements (A.10), (A.11) to also include expressions containing metavariable contexts 𝑀;Γ ⊢ 𝑡 ∶ α.

In a similar way, we can repeat this for Box: given contexts 𝑀 and Γ we can define a typing judgement 𝑀;Γ ⊢ 𝑏 ∶ β where 𝑏 : Box and β is a type. The inference rules for this are given in (3.13). These have been chosen to mirror the typings given in Section 2.4.3.

These typing rules have been designed to match the typing rules (A.10) of the underlying proof terms that a Box produces when solved, as I will show next.

3.4.3. Results of a Box

The structure of Box is designed to represent a partially complete expression without the use of unbound metavariables. Boxes can be converted to expressions containing unbound metavariables using results : Box → Set Expr as defined in (3.14).

results
  : Box           → Set Expr
  | ℐ (𝑥∶α) 𝑏     ↦ {(Expr.λ (𝑥∶α) 𝑟[𝑥]) for 𝑟 in results 𝑏}
  | 𝒢 (𝑥∶α) 𝑏     ↦ results 𝑏
  | 𝒭 𝑡           ↦ {𝑡}
  | 𝒜 𝑏₁ (𝑥∶α) 𝑏₂ ↦
    {𝑠 for 𝑠 in results ⦃𝑥 ↦ 𝑟⦄ 𝑏₂
       for 𝑟 in results 𝑏₁}
  | 𝒪 𝑏₁ 𝑏₂       ↦ results 𝑏₁ ∪ results 𝑏₂
  | 𝒱 (𝑥∶α) 𝑏     ↦ {(Expr.let 𝑥 𝑏 𝑟) for 𝑟 in results 𝑏}

A 𝑏 : Box is solved when there are no remaining 𝒢 entries in it. When 𝑏 is solved, the set of results for 𝑏 does not contain any metavariables and hence can be checked by the kernel. In the case that 𝑏 is unsolved, the results of 𝑏 contain unbound metavariables. Each of these metavariables corresponds to a 𝒢-binder that needs to be assigned.

Lemma 3.15 (compatibility): Suppose that 𝑀;Γ ⊢ 𝑏 : α for 𝑏 : Box as defined in (3.13). Then [..𝑀, ..goals 𝑏];Γ ⊢ 𝑟 ∶ α. (Say that 𝑏 is compatible with 𝑟 ∈ results 𝑏.) Here, goals 𝑏 is the set of metavariable declarations formed by accumulating all of the 𝒢-binders in 𝑏. (3.16) shows a formal statement of Lemma 3.15.

Lemma 3.15 states that given a box 𝑏 and an expression 𝑟 that is a result of 𝑏, then if 𝑏 is a valid box with type α then 𝑟 will type to α too in the metavariable context including all of the goals in 𝑏.

Lemma 3.15 is needed because it ensures that our Box will produce well-typed expressions when solved. Using Lemma 3.15, we can find box-tactics m : Box → Option Box - partial functions from Box to Box - such that 𝑀;Γ ⊢ 𝑏 ∶ α ⇒ 𝑀;Γ ⊢ m 𝑏 ∶ α whenever 𝑏 ∈ dom m. Hence a chain of such box-tactic applications will produce a result that satisfies the initial goal.

Proof: Without loss of generality, we only need to prove Lemma 3.15 for a 𝑏 : Box with no 𝒪 boxes and a single result [𝑟] = results 𝑏. To see why, note that any box containing an 𝒪 can be split as in (3.17) until each Box has one result. Then we may prove Lemma 3.15 for each of these in turn.

Write result 𝑏 to mean this single result 𝑟. Performing induction on the typing judgements for boxes, the most difficult is 𝒜-typing, where we have to show (3.18).

where 𝑀' := [..𝑀, ..goals (𝒜 𝑏₁ (𝑥∶α) 𝑏₂)]. To derive this it suffices to show that result is a 'substitution homomorphism':

where σ is a substitutionSee Section 2.4.1. A substitution is a partial map from variables to expressions. in context Γ and ≡ is the definitional equality judgement under Γ. Then we have

𝑀';Γ ⊢
  result (𝒜 𝑏₁ (𝑥∶α) 𝑏₂)
  ≡ result (⦃𝑥 ↦ result 𝑏₁⦄ 𝑏₂)
  ≡ ⦃𝑥 ↦ result 𝑏₁⦄ (result 𝑏₂)
  ≡ (λ (𝑥∶α), result 𝑏₂) (result 𝑏₁)

We can see the substitution homomorphism property of result holds by inspection on the equations of result, observing that each LHS expression behaves correctly. Here is the case for ℐ:

𝑀';Γ ⊢
  result (σ (ℐ (𝑥∶α) 𝑏))
  ≡ result $ ℐ (𝑥∶(σ α)) (σ 𝑏)
  ≡ (λ (𝑥∶(σ α)), (result (σ 𝑏))[𝑥])
  ≡ (λ (𝑥∶(σ α)), (σ (result 𝑏))[𝑥]) -- ∵ induction hypothesis
  ≡ σ (λ (𝑥∶α), (result 𝑏))
  ≡ σ (result (ℐ (𝑥∶α) 𝑏))

This completes the proof of Lemma 3.15. By using compatibility, we can determine whether a given box-tactic m : Box → Option Box is sound. Define a box-tactic m to be sound when for all 𝑏 ∈ dom m we have some α such that 𝑀;Γ ⊢ (m 𝑏) ∶ α whenever 𝑀;Γ ⊢ 𝑏 ∶ α.

Hence, to prove a starting propositionOr, in general, a type α. P, start with an initial box 𝑏₀ := 𝒢 (?t₀∶P) (𝒭 ?t₀). Then if we only map 𝑏₀ with sound box-tactics to produce a solved box 𝑏ₙ, then each of results 𝑏ₙ always has type α and hence is accepted by Lean's kernel.

Given a box-tactic m that is sound on 𝑏, then we can construct a sound box-tactic on ℐ (𝑥∶α) 𝑏 too that acts on the nested box 𝑏.

3.4.4. Escape-hatch to tactics

As discussed in Section 2.4.4, many provers, including Lean 3, come with a tactic combinator language to construct proofs through mutating an object called the TacticState comprising a metavariable context and a list of metavariables called the goals. In Section 3.1 I highlighted some of the issues of this approach, but there are many built-in and community-made tactics which can still find use within a HumanProof proof. For this reason, it is important for HumanProof to provide an 'escape hatch' allowing these tactics to be used within the context of a HumanProof proof seamlessly. I achieve this compatibility system between Boxes and tactics through defining a zipper [Hue97[Hue97]Huet, GérardFunctional Pearl: The Zipper (1997)Journal of functional programminghttp://www.st.cs.uni-sb.de/edu/seminare/2005/advanced-fp/docs/huet-zipper.pdf] structure on Boxes (Appendix A.2) and then a set of operations for soundly converting an underlying TacticState to and from a Box object. The details of this mechanism can be found in Appendix A.2. It is used to implement some of the box-tactics presented next in Section 3.5, since in some cases the box-tactic is the same as its tactic-based equivalent.

3.4.5. Summary

In this section, I defined assignability on Boxes and the valid typing judgement inference rules on Box. I used these to define the soundness of a box-tactic and showed that for a box-tactic to be sound, it suffices to show that its typing judgement is preserved through the use of Lemma 3.15. I also briefly review Appendix A, which presents a mechanism for converting a tactic-style proof to a box-tactic.

3.5. Human-like-tactics for Box.

Using the framework presented above we can start defining sound tactics on Boxes and use Box to actualise the kinds of reasoning discussed in Section 3.1. Many of the box-tactics here are similar to inference rules that one would find in a usual system, and so I do not cover these ones in great detail. I also skip many of the soundness proofs, because in Appendix A I instead provide an 'escape hatch' for creating sound box-tactics from tactics in the underlying metavariable-oriented development calculus.

3.5.1. Simplifying box-tactics

We have the following box-tactics for reducing Boxes, these should be considered as tidying box-tactics.

3.5.2. Deleting tactics

These are box-tactics that cause a Box to become simpler, but which are not always 'safe' to do, in the sense that they may lead to a Box which is impossible to solve. That is, the Box may still have a true conclusion but it is not possible to derive this from the information given on the box. For example, deleting a hypothesis 𝑝 ∶ P, may prevent the goal ?𝑡 ∶ P from being solved. The rules for deletion are presented in (3.23).

To motivate 𝒪-revert tactics, recall that an 𝒪-box 𝑏₁ ⋁ 𝑏₂ represents the state that either 𝑏₁ or 𝑏₂ needs to be solved, so 𝒪-reversion amounts to throwing away one of the boxes. This is similar to 𝒪-reduce in (3.22) with the difference being that we do not need one of the boxes to be solved before applying. These are useful when it becomes clear that a particular 𝒪-branch is not solvable and can be deleted.

3.5.3. Lambda introduction

In tactics, an intro tactic is used to introduce Π-bindersΠ-binders Π (𝑥 : α), β are the dependent generalisation of the function type α → β where the return type β may depend on the input value α.. That is, if the goal state is ⊢ Π (𝑥 : α), β[𝑥] the intro tactic produces a new state (𝑥 : α) ⊢ β[𝑥]. To perform this, it assigns the goal metavariable ?t₁ : Π (𝑥 : α), β[𝑥] with the expression λ (𝑥 : α), ?t₂ where ?t₂ : β[𝑥] is the new goal metavariable with context including the additional local variable 𝑥 : α.

The intro tactic on Box is analogous, although there are some additional steps required to ensure that contexts are preserved correctly. The simplified case simple_intro (3.24), performs the same steps as the tactic version of intro.

The full version (3.25) is used in the case that the ℐ-box is not immediately followed by an 𝒭-box. In this case, a conjunctive 𝒜-box must be created in order to have a separate context for the new (𝑥 : α) variable.

The fact that intro is sound follows mainly from the design of the definitions of ℐ:

Structural sharing is defined as making use of the same substructure multiple times in a larger structure. For example, a tree with two branches being the same would be using structural sharing if the sub-branches used the same object in memory. Define 𝑏' to be ℐ (𝑥 : α), 𝒢 (?t₁ : β), 𝒭 ?t₁, represented graphically in (3.26). The typing judgement (3.26) follows from the typing rules (3.13).

By the definition of a sound box-tactic we may assume ⊢ (𝒢 ?t₀, 𝑏) : γ for some type γ. From the 𝒢 typing rule (3.13) we then have [?t₀];∅ ⊢ 𝑏 : γ. Then it follows from 𝒜 typing (3.13) that ⊢ 𝒜 𝑏' (t₀ : Π (𝑥 : α), β) 𝑏 : γ where 𝑏' := ℐ (𝑥 : α), 𝒢 (?t₁ : β), 𝒭 ?t₁.

3.5.4. Split and cases tactics

Here I present some box-tactics for performing introduction and elimination of the ∧ type. The Box version of split performs the same operation as split in Lean: introducing a conjunction. A goal ?t₀ : P ∧ Q is replaced with a pair of new goals (?t₁,?t₂). These can be readily generalised to other inductive datatypes with one constructorOne caveat is that the use of ∃ requires the use of a non-constructive axiom of choice with this method. This is addressed in Section 3.5.8. In the implementation, these are implemented using the tactic escape-hatch described in Appendix A.

Similarly we can eliminate a conjunction with cases.

3.5.5. Induction box-tactics

∧-elimination (3.28) from the previous section can be seen as a special case of induction on datatypes. Most forms of dependent type theory use inductive datatypes (see Section 2.2.3) to represent data and propositions, and use induction to eliminate them. To implement induction in CICCalculus of Inductive Constructions. The foundation used by Lean 3 and Coq (Section 2.1.3). See [Car19 §2.6] for the axiomatisation of inductive types within Lean 3's type system., each inductive datatype comes equipped with a special constant called the recursor. This paradigm broadens the use of the words 'recursion' and 'induction' to include datastructures that are not recursive.

For example, we can view conjunction A ∧ B : Prop as an inductive datatype with one constructor mk : A → B → A ∧ B. Similarly, a disjunctive A ∨ B has two constructors inl : A → A ∨ B and inr : B → A ∨ B. Interpreting → as implication, we recover the basic introduction axioms for conjunction and disjunction. The eliminators for ∧ and ∨ are implemented using recursors given in (3.29).

∧-rec : ∀ (A B C : Prop), (A → B → C) → (A ∧ B) → C
∨-rec : ∀ (A B C : Prop), (A → C) → (B → C) → (A ∨ B) → C

Performing an induction step in a CIC theorem prover such as Lean amounts to the application of the relevant recursor. Case analysis on a disjunctive hypothesis makes for a good example of recursion, the recursor ∨-rec : (P → C) → (Q → C) → (P ∨ Q) → C is used. Given a box ℐ (h₀ : P ∨ Q), 𝑏 where h₀ ⊢ 𝑏 ∶ α, the ∨-cases box-tactic sends this to the box defined in (3.30). This is visualised in (3.31).

𝒜 (ℐ (h₁∶P), 𝑏₁) (𝑐₁∶P → α) (
  𝒜 (ℐ (h₂∶Q), 𝑏₂) (𝑐₂∶Q → α) (
    𝒭 (∨-rec 𝑐₁ 𝑐₂ h₀)
  )
)
where 𝑏₁ := ⦃h₀ ↦ inl h₁⦄ 𝑏
      𝑏₂ := ⦃h₀ ↦ inr h₂⦄ 𝑏

Note that the 𝑏 : Box in (3.31) may contain multiple goals. When the cases box-tactic is applied to ℐ (h₀∶P ∨ Q), 𝑏, the resulting Box on the rhs of (3.31) results in two copies of these goals. This implements structural sharing of goals as motivated in Section 3.1.3. Structural sharing has a significant advantage over the goal-state style approach to tactics, where the equivalent cases tactic would have to be applied separately to each goal if there were multiple goals.

This structurally-shared induction step also works on recursive datastructures such as lists and natural numbers. These datatypes' recursors are more complicated than non-recursive datastructures such as those in (3.29) in order to include induction hypotheses. The recursor for natural numbers is shown in (3.32). (3.33) is the corresponding box-tactic that makes use of (3.32). (3.34) is the detailed Box structure for the right-hand side of (3.33).

ℕ-rec :
  (𝒞 : ℕ → Type)                   -- motive
  → (𝒞 0)                          -- zero case
  → ((𝑖 : ℕ) → 𝒞 𝑖 → 𝒞 (𝑖 + 1))  -- successor case
  → (𝑖 : ℕ) → 𝒞 𝑖

𝒜 (⦃𝑛 ↦ 0⦄𝑏) (𝑐₁ ∶ ⦃𝑛 ↦ 0⦄α) (
  𝒜 (ℐ (𝑛 ∶ ℕ), ℐ (𝑕 ∶ α), ⦃𝑛 ↦ 𝑛+1⦄𝑏) (𝑐₂∶ ⦃𝑛 ↦ 𝑛+1⦄α) (
    𝒭 (ℕ-rec (𝑛 ↦ α) 𝑐₁ 𝑐₂ 𝑛)
  )
)

In general, finding the appropriate motive 𝒞 for an induction step amounts to a higher order unification problem which was shown to be undecidable [Dow01[Dow01]Dowek, GilesHigher-order unification and matching (2001)Handbook of automated reasoninghttps://who.rocq.inria.fr/Gilles.Dowek/Publi/unification.ps §3]. However, in many practical cases 𝒞 can be found and higher-order provers come equipped with heuristics for these cases, an early example being Huet's semidecidable algorithm. Rather than reimplementing these heuristics, I implement induction box-tactics on Box by using the 'escape hatch' feature (Section 3.4.4).

3.5.6. Introducing 𝒪 boxes

The purpose of 𝒪 boxes is to enable backtracking and branches on Boxes that enables structural sharing. The G&G prover [GG17[GG17]Ganesalingam, Mohan; Gowers, W. T.A fully automatic theorem prover with human-style output (2017)Journal of Automated Reasoninghttps://doi.org/10.1007/s10817-016-9377-1] takes a similar approach. For example, suppose that we had a goal x ∈ A ∪ B for some sets A, B. We might have some lemmas of the form h₁ : P → x ∈ A and h₂ : Q → x ∈ B but we are not yet sure which one to use. In a goal-based system, if you don't yet know which injection to use, you have to guess and manually backtrack. However, there may be some clues about which lemma is correct that only become apparent after applying an injection. In the above example, if only h₃ : P is present as a hypothesis, it requires first performing injection before noticing that h₁ is the correct lemma to apply. In Section 3.7.1 I discuss more advanced, critic-like workflows that 𝒪-boxes also enable.

The 𝒪 box allows us to explore various counterfactuals without having to perform any user-level backtracking (that is, having to rewrite proofs). The primitive box-tactic that creates new 𝒪-boxes is shown in (3.35). This is used to make more 'human-like' box-tactics such as ∨-split (3.36).

3.5.7. Unification under a Box

Unification is the process of taking a pair of expressions 𝑙 𝑟 : Expr within a joint context 𝑀;Γ and finding a valid set of assignments of metavariables σ in 𝑀 such that (𝑀 + σ);Γ ⊢ 𝑙 ≡ 𝑟. Rather than develop a whole calculus of sound unification for the Box system, I can use the 'escape hatch' tactic compatibility layer developed in Appendix A to transform a sub-Box to a metavariable context and then use the underlying theory of unification used for the underlying development calculus of the theorem prover (in this case Lean). This is a reasonable approach because unifiers and matchers for theorem provers are usually very well developed in terms of both features and optimisation, so I capitalise on a unifier already present in the host proof assistant has a perfectly good one already.

3.5.8. Apply

In textbook proofs of mathematics, often an application of a lemma acts under ∃ binders. For example, let's look at the application of fs 𝑛 being continuous from earlier.

h₁ :
  ∀ (𝑥 : X) (ε : ℝ) (h₀ : ε > 0),
    ∃ (δ : ℝ) (h₁ : δ > 0),
      ∀ (𝑦 : X) (h₂ : dist 𝑥 𝑦 < δ), dist (f 𝑥) (f 𝑦) < ε

In the example the application of h₁ with 𝑁, ε, h₃, and then eliminating an existential quantifier δ and then applying more arguments y, all happen in one step and without much exposition in terms of what δ depends on. A similar phenomenon occurs in backwards reasoning. If the goal is dist (f 𝑥) (f 𝑦) < ε, in proof texts the continuity of f is applied in one step to replace this goal with dist x y < δ, where δ is understood to be an 'output' of applying the continuity of f.

Contrast this with the logically equivalent Lean tactic script fragment (3.38):

...
show dist (f x) (f y) < ε,
obtain ⟨δ, δ_pos, h₁⟩ : ∃ δ, δ > 0 ∧ ∀ y, dist x y < δ → dist (f x) (f y) < ε,
  apply ‹continuous f›,
apply h₁,
show dist x y < δ,
...

In order to reproduce this human-like proof step, we need to develop a theory for considering 'complex applications'. A further property we desire is that results of the complex application must be stored such that we can recover a natural language write-up to explain it later (e.g., creating "Since f is continuous at x, there is some δ...").

The apply subsystem works by performing a recursive descent on the type of the assumption being applied. For example, applying the lemma given in (3.37) to a goal 𝑡 : P attempts to unify P with dist (f ?𝑥) (f ?𝑦) < ?ε with new metavariables ?𝑥 ?𝑦 : X, ε : ℝ. If the match is successful, it will create a new goal for each variable in a Π-binderNote that ∀ is sugar for Π. above the matching expression and a new 𝒱-binder for each introduced ∃-variable and each conjunct. These newly introduce nested boxes appear in the same order as they appear in the applied lemma.

This apply system can be used for both forwards and backwards reasoning box-tactics. Above deals with the backwards case, in the forwards case, the task is reversed, with now a variable bound by a Π-binder being the subject to match against the forwards-applied hypothesis.

An example of applying (3.37) to the goal dist (f x) (f y) < ε can be seen in (3.1).

3.5.8.1. A note on using apply with existential statements

One complication with this approach to apply is performing many logical inference steps when applying a lemma in one go. There is a technical caveat with applications of existential statements such as ∃ (δ : ℝ), d(𝑥, 𝑦) < δ: by default, Lean is a non-classical theorem prover, which here amounts to saying that the axiom of choice is not assumed automatically. Without the axiom of choice, it is not generally possible to construct a projection function ε : ∃ (𝑥 : α), P [𝑥] → α such that P[ε ℎ] is true for all ℎ : ∃ (𝑥 : α), P. There are two ways to overcome this limitation:

1. Assume the axiom of choice and make use of the nonconstructive projector ε.

2. When an apply step encounters an existential quantifier, wrap the entire proof in an existential quantifier recursorRecursors are discussed in Section 3.5.5. ∃-rec (C : Prop) : (∀ (𝑥 : α), P 𝑥 → C) → (∃ (𝑥 : α), P 𝑥) → C using 𝒜-boxes. This is performed in exactly the same manner that induction box-tactics are applied in Section 3.5.5.

HumanProof, as it is currently implemented, uses strategy 1. This prevents proofs from being constructive, but is otherwise not so great a concession, since mathematicians regularly make use of this in fields outside logic. There was some effort to also implement strategy 2, but I dropped it.

3.5.9. Summary

This section introduced a set of sound box-tactics that are implemented for the HumanProof system. In the next section we will see how these box-tactics can be used to create natural language write-ups of proofs.

3.6. Natural language generation of proofs

In this section I detail how the above box architecture is used to produce natural language writeups as the proof progresses. The general field is known as Natural Language Generation (NLG). You can find a background survey of NLG both broadly and within the context of generating proofs in Section 2.7.

Here I lean on the work of Ganesalingam, who in his thesis [Gan10[Gan10]Ganesalingam, MohanThe language of mathematics (2010)PhD thesis (University of Cambridge)http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.211.9027&rep=rep1&type=pdf] has specified a working theory of the linguistics of natural language mathematics. As well as generating a formally verifiable result of a proof, I also extend on G&G by providing some new mechanisms for converting Lean predicates and typeclasses in to English language sentences. That is, in the implementation of the G&G theorem prover, many natural language constructs such as "$X$ is a metric space" were hard-coded in to the system. In this work I provide a general framework for attaching verbalisations of these kinds of statements to typeclasses and predicates within Lean. I also make the resulting write-up interactive; emitting a partial proof write-up if the proof-state is not yet solved and also inspecting the natural language write-up through the widgets system are possible. In contrast G&G's output was a static $\text{LATEX}$ file.

The goal of this section is to demonstrate that the Box architecture above is representative of human-like reasoning by constructing natural language writeups of the proofs created using Boxes. As such the NLG used here is very simple compared to the state of the art and doesn't make use of any modern techniques such as deep learning. The output of this system is evaluated by real, human mathematicians in Chapter 6. An example of a proof generated by the system is shown below in Output 3.40. There are some challenges in converting a Box proof to something that reads like a mathematical proof that I will detail here.

3.6.1. Overview

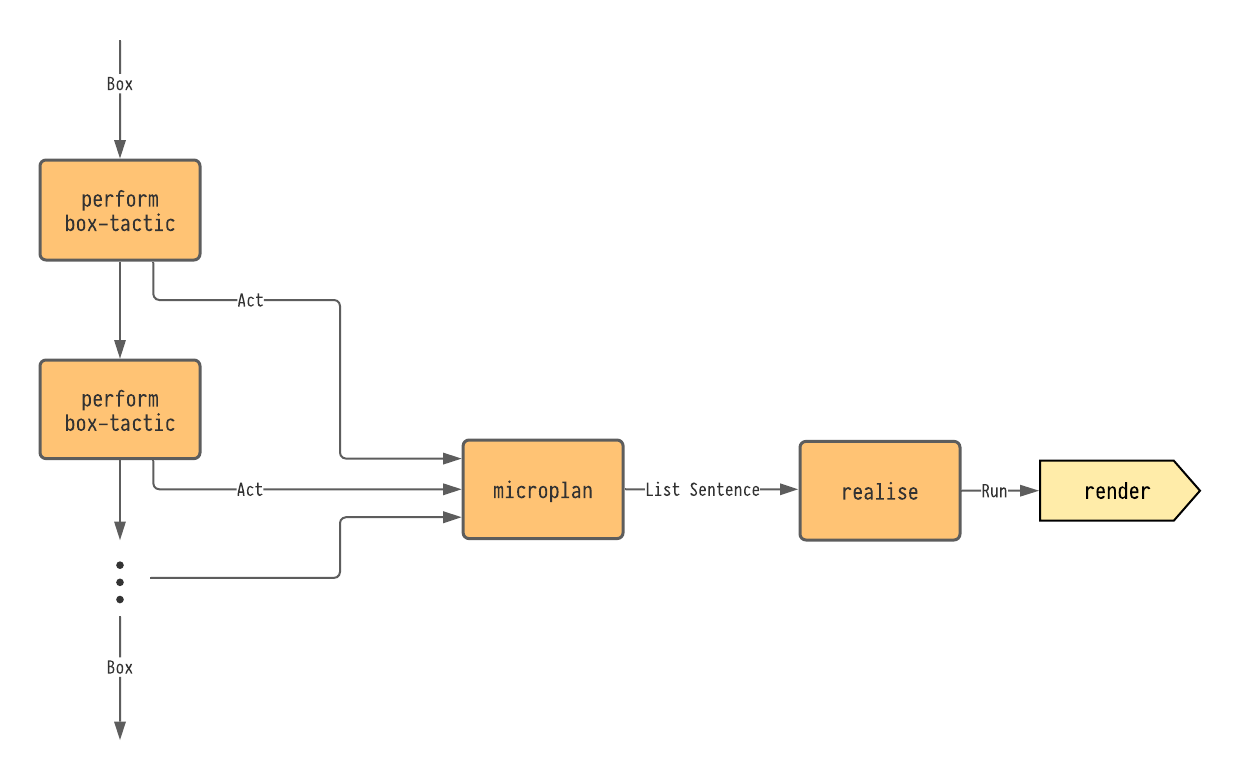
The architecture of the NLG component is given in Figure 3.41. The design is similar to the standard architecture discussed in Section 2.7.1. In Section 3.1.2 I explained the decision to design the system to permit only a restricted set of box-tactics on a Box representing the goal state of the prover. To create the natural language write-up from these box-tactics, each box-tactic also emits an Act object. This is an inductive datatype representing the kind of box-tactic that occurred. So for example, there is an Intro : List Binder → Act that is emitted whenever the intro box-tactic is performed, storing the list of binders that were introduced. A list of Acts is held in the state monad for the interactive proof session. This list of acts is then fed to a micro-planner, which converts the list of acts to an abstract representation of sentencesSometimes referred to as a phrase specification. These sentences are converted to a realised sentence with the help of Run which is a form of S-expression [McC60[McC60]McCarthy, JohnRecursive functions of symbolic expressions and their computation by machine, Part I (1960)Communications of the ACMhttps://doi.org/10.1145/367177.367199] containing text and expressions for interactive formatting. This natural language proof is then rendered in the output window using the widgets system (Chapter 5).

3.6.2. Grice's laws of implicature

One resource that has proven useful in creating human-like proofs is the work of the Grice on implicature in linguistics [Gri75[Gri75]Grice, Herbert PLogic and conversation (1975)Speech actshttp://rrt2.neostrada.pl/mioduszewska/course_265_reading%201b.pdf]. To review, Grice states that there is an unwritten rule in natural languages that one should only provide as much detail as is needed to convey the desired message. For example, the statement "I can't find my keys" has the implicature "Do you know where my keys are?", it implies that the keys may have been lost at the current location and not in a different part of town and so on. If superfluous detail is included, the reader will pick this up and try to use it to infer additional information. Saying "I can't find my keys at the moment" interpreted literally has the same meaning as "I can't find my keys", but implicitly means that I have only just realised the key loss or that I will be able to find them soon. Grice posits four maxims that should be maintained in order for a sentence or phrase to be useful:

1. Quantity The contribution should contain no more or less than what is required. Examples: "Since $x>5$ and $x$ is prime, $x>6$". "Let $x$ be a positive real such that $x>0$."

2. Quality Do not say things for which you don't have enough evidence or things that are not true. An example here would be a false proof.

3. Relation The contributed sentence should be related to the task at hand. Example; putting a true but irrelevant statement in the middle of the proof is bad.

4. Manner The message should avoid being obscure, ambiguous and long-winded.

Mathematical texts are shielded from the more oblique forms of implicature that may be found in general texts, but Grice's maxims are still important to consider in the construction of human-readable proofs and serve as a useful rule-of-thumb in determining when a generated sentence will be jarring to read.

With respect to the quantity maxim, it is important to remember also that what counts as superfluous detail can depend on the context of the problem and the skill-level of the reader. For example, one may write:

Suppose $A$ and $B$ are open subsets of $X$. Since $f$ is continuous, $f^{-1}[A\cup B]$ is open.

A more introductory text will need to also mention that $X$ is a topological space and so $A\cup B$ is open. Generally these kinds of implicit lemma-chaining can become arbitrarily complex, but it is typically assumed that these implicit applications are entirely familiar to the reader. Mapping ability level to detail is not a model that I will attempt to write explicitly here. One simple way around this is to allow the proof creator to explicitly tag steps in the proof as 'trivial' so that their application is suppressed in the natural language write-up. Determining this correct level of detail may be a problem in which ML models may have a role to play.

3.6.3. Microplanning symbolic mathematics

From a linguistic perspective, a remarkable property of mathematical texts is the interlacing of mathematical symbols and natural language. In the vast majority of cases, each symbolic construct has a natural language equivalent (else verbalising that symbol in conversation would be difficult). For example: "$x+y$" versus "$x$ plus $y$". Sometimes multiple verbalisations are possible: $P\Rightarrow Q$ can be "$P$ implies $Q$" or "$Q$ whenever $P$". Sometimes the the symbolic form of a statement is not used as frequently: "$p$ is prime" versus $p\in P$. In making text flow well, the decision of when to move between symbolic and textual renderings of a mathematical proof is important. The rule-of-thumb that I have arrived at is to render the general flow of the proof's reasoning using text and to render the objects that are being reasoned about using symbols. The idea here is that one should be able to follow the rough course of argument whilst only skimming the symbolic parts of the proof.

3.6.4. Microplanning binders with class predicate collections

In mathematics, it is common that a variable will be introduced in a sentence and then referenced in later sentences. For example, one will often read sentences such as "Let $X$ be a metric space and let $x$ and $y$ be points in $X$". This corresponds to the following telescopeA telescope is a list of binders where the type of a binder may depend on variables declared ealier in the list. Telescopes are equivalent to a well-formed context (see Section 2.1.3) but the term telescope is also used to discuss lists of binders that appear in expressions such as lambda and forall bindings. of binders: (X : Type) (_ : metric_space X) (x y : X). These effectively act as 'linguistic variable binders'.

In this subsection I will highlight how to convert lists of binders to natural language phrases of this form. To the best of my knowledge this is an original contribution so I will explain this mechanism in more detail. This approach is inspired by the idea of 'notions' as first used in the ForTheL controlled natural language parser for the SAD project [VLP07[VLP07]Verchinine, Konstantin; Lyaletski, Alexander; Paskevich, AndreiSystem for Automated Deduction (SAD): a tool for proof verification (2007)International Conference on Automated Deductionhttps://doi.org/10.1007/978-3-540-73595-3_29, Pas07[Pas07]Paskevich, AndreiThe syntax and semantics of the ForTheL language (2007)PhD thesis (Université Paris XII)http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.211.8865&rep=rep1&type=pdf, VLPA08[VLPA08]Verchinine, Konstantin; Lyaletski, Alexander; Paskevich, Andrei; et al.On correctness of mathematical texts from a logical and practical point of view (2008)International Conference on Intelligent Computer Mathematicshttps://doi.org/10.1007/978-3-540-85110-3_47] also used by Naproche/SAD [DKL20[DKL20]De Lon, Adrian; Koepke, Peter; Lorenzen, AntonInterpreting Mathematical Texts in Naproche-SAD (2020)Intelligent Computer Mathematicshttps://doi.org/10.1007/978-3-030-53518-6_19]. Ganesalingam [Gan10[Gan10]Ganesalingam, MohanThe language of mathematics (2010)PhD thesis (University of Cambridge)http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.211.9027&rep=rep1&type=pdf] refers to these as non-extensional types and Ranta [Ran94[Ran94]Ranta, AarneSyntactic categories in the language of mathematics (1994)International Workshop on Types for Proofs and Programshttps://doi.org/10.1007/3-540-60579-7_9] as syntactic categories. The act of The PROVERB system [HF97[HF97]Huang, Xiaorong; Fiedler, ArminProof Verbalization as an Application of NLG (1997)International Joint Conference on Artificial Intelligencehttp://ijcai.org/Proceedings/97-2/Papers/025.pdf] and the G&G system [GG17[GG17]Ganesalingam, Mohan; Gowers, W. T.A fully automatic theorem prover with human-style output (2017)Journal of Automated Reasoninghttps://doi.org/10.1007/s10817-016-9377-1] provide a mechanism for generating natural language texts using a similar technique for aggregating assumptions, however these approaches do not allow for the handling of more complex telescopes found in dependent type theory. Table 3.42 presents some examples of the kinds of translations in question.

[HHPW96]Hall, Cordelia V; Hammond, Kevin; Peyton Jones, Simon L; et al.Type classes in Haskell (1996)ACM Transactions on Programming Languages and Systems (TOPLAS)https://doi.org/10.1145/227699.227700[MAKR15]de Moura, Leonardo; Avigad, Jeremy; Kong, Soonho; et al.Elaboration in Dependent Type Theory (2015)CoRRhttp://arxiv.org/abs/1505.04324The variable introduction sentences in Table 3.42 take the role of a variable binder for mathematical discourse. This variable is then implicitly 'in scope' until its last mention in the text. Some variables introduced in this way can remain in scope for an entire book. For example, the choice of underlying field k in a book on linear algebra. As Ganesalingam notes [Gan10[Gan10]Ganesalingam, MohanThe language of mathematics (2010)PhD thesis (University of Cambridge)http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.211.9027&rep=rep1&type=pdf §2.5.2], "If mathematicians were not able to use variables in this way, they would need to write extremely long sentences!"

Let's frame the problem as follows: take as input a telescope of binders (e.g, [(𝑎 : ℤ), (𝑏 : ℤ), (h₁ : coprime 𝑎 𝑏)]) and produce a 'variable introduction text' string as shown in the above table. The problem involves a number of challenges:

• There is not a 1-1 map between binders and pieces of text: in "Let 𝑎, 𝑏 be coprime", the binder h₁ : coprime 𝑎 𝑏 is not named but instead treated as a property of 𝑎 and 𝑏.

• The words that are used to describe a variable can depend on which typeclass [HHPW96]See the caption of Table 3.42 for more information on typeclasses. their type belongs to. For instance, we write "let 𝑥 and 𝑦 be points" or "let 𝑥 and 𝑦 be elements of G" depending on whether the type of 𝑥 and 𝑦 is an instance of group or metric_space.

• Compare "𝑥 and 𝑦 are prime" versus "𝑥 and 𝑦 are coprime". The first arises from (𝑥 𝑦 : ℕ) (h₁ : prime 𝑥) (h₂ : prime 𝑦) whereas the second from (𝑥 𝑦 : ℕ) (h₁ : coprime 𝑥 𝑦). Hence we need to model the adjectives "prime" and "coprime" as belonging to distinct categories.

To solve this I introduce a schema of class predicate collections. Each binder in the input telescope is converted to two pieces of data; the subject expression 𝑥 and the class predicate 𝑐𝑝; which is made from one of the following constructors.

• adjective: "continuous", "prime", "positive"

• fold_adjective: "coprime", "parallel"

• symbolic_postfix: "∈ A", "> 0", ": X → Y"

• class_noun: "number", "group", "points in X", "elements of G", "function", "open set in T"

• none: a failure case. For example, if the binder is just for a proposition that should be realised as an assumption instead of a predicate about the binder.

The subject expression and the class predicate for a given binder in the input telescope are assigned by consulting a lookup table which pattern-matches the binder type expressions to determine the subject expression and any additional parameters (for example T in "open set in T"). Each pair ⟨𝑥, 𝑐𝑝⟩ is mapped to ⟨[𝑥], [𝑐𝑝]⟩ : List Expr × List ClassPredicate. I call this a class predicate collection (CPC). The resulting list of CPCs is then reduced by aggregating [DH93[DH93]Dalianis, Hercules; Hovy, EduardAggregation in natural language generation (1993)European Workshop on Trends in Natural Language Generationhttps://doi.org/10.1007/3-540-60800-1_25] adjacent pairs of CPCs according to (3.43).

⟨𝑥𝑠, 𝑐𝑝𝑠 ⟩, ⟨𝑦𝑠, 𝑐𝑝𝑠 ⟩ ↝ ⟨𝑥s ++ 𝑦𝑠, 𝑐𝑝𝑠⟩
⟨𝑥𝑠, 𝑐𝑝𝑠₁⟩, ⟨𝑥𝑠, 𝑐𝑝𝑠₂⟩ ↝ ⟨𝑥s, 𝑐𝑝𝑠₁ ++ 𝑐𝑝𝑠₂⟩

In certain cases, the merging operation can also delete class predicates that are superseded by later ones. An example is that if we have (𝑥 : X) (h₁ : 𝑥 ∈ A), this can be condensed directly to ⟨[𝑥], [symbolic_postfix "∈ A"]⟩ which realises to "Let 𝑥 ∈ A" instead of the redundant "Let 𝑥 ∈ A be an element of X" which violates Grice's maxim of quantity (Section 3.6.2).

Additionally, the resulting class predicate collection list is partitioned into two lists so that only the first mention of each subject appears in the first list. For example; 𝑥 : X and h : 𝑥 ∈ A both have the subject 𝑥, but "Let 𝑥 be a point and let 𝑥 ∈ A"

These class predicate collections can then be realised for a number of binder cases:

• Let: "Let U be open in X"

• Forall: "For all U open in X"

• Exists: "For some U open in X"

class_noun can be compared to the concept of a 'notion' in ForTheL and Naproche/SAD and a 'non-extensional type' in Ganesalingam [Gan10[Gan10]Ganesalingam, MohanThe language of mathematics (2010)PhD thesis (University of Cambridge)http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.211.9027&rep=rep1&type=pdf]. It takes the role of a noun that the introduced variable belongs to, and is usually preceded with an indefinite article: "let 𝑥 be an element of G".

Will some mechanism like CPCs be necessary in the future, or are they a cultural artefact of the way that mathematics has been done in the past? When designing mathematical definitions in formalised mathematics, one must often make a choice in how new datatypes are defined: should there be a new type 'positive real number' or just use the real numbers ℝ and add a hypothesis ε > 0? In natural language mathematics, one is free to move between these bundled and unbundled representations without concern. The CPC structure reflects this; "ε is a positive real" can be interpreted as either a "real that is positive" or as a single semantic type "positive real". Natural mathematics does not disambiguate between these two because they are both equivalent within its informal rules, similar to how the representation of 𝑎 + 𝑏 + 𝑐 does not need to disambiguate between (𝑎 + 𝑏) + 𝑐 and 𝑎 + (𝑏 + 𝑐) since they are equal.

3.6.5. Handling 'multi-apply' steps

The specialised apply box-tactic discussed in Section 3.5.8 requires some additional processing. The apply box-tactic returns a datatype called ApplyTree that indicates how a given lemma was applied, resulting in parameters, goals and values obtained through eliminating an existential statement. These are converted in to "since" sentences:

"Since f is continuous, there exists some δ > 0 such that d (f 𝑥) (f 𝑦) < 0 whenever d 𝑥 𝑦 < δ"

The code that produces this style of reasoning breaks down in to a Reason component indicating where the fact came from and a restatement of the fact with the parameters set to be relevant to the goal. In most cases, the Reason can simply be a restatement of the fact being used. However, it is also possible to produce more elaborate reasons. For example, apply ℎ for some hypothesis ℎ will also match preconditions on ℎ if they appear in context. That is, if h₀ ∶ P → Q, then apply h₀ in the box in (3.44) will automatically include the propositional assumption h₁ : P to solve the Box, instead of resulting in a new goal ?t₂ : P. This will produce the reason "Since P → Q and P, we have Q".

3.6.6. Multiple cases

Some problems branch into multiple cases. For example, the A ∪ B problem. Here, some additional macroplanning needs to occur, since it usually makes sense to place each of the cases in their own paragraph. When cases is performed, the resulting 𝒜-box contains two separate branches for each case as discussed in (3.28).

When a new box-tactic is performed to create an Act, box-tactics that are performed within one of these case blocks causes the Act to be tagged with the case. This is then used to partition the resulting rendered string into multiple paragraphs.

3.6.7. Realisation

As shown in Figure 3.41, the set of Acts is compiled to a sequence of Sentence objects and these are converted to a run of text. As detailed in Section 2.7 this last step is called realisation. In the realisation phase, each sentence is converted to a piece of text containing embedded mathematics. Each statement is constructed through recursively assembling canned phrases representing each sentence. This means that longer proofs can become monotonous but the application of synonymous phrases could be used to add variation. However, the purpose of this NLG system is to produce 'human-like' reasoning and so if the proofs read as too monotonous, it suggests that less detail should have been included in the Act list structure.

When realising logical statements, the prose would become unnatural or ambiguous after a certain depth. After a depth of two these statements switch to being entirely symbolic. For example: (P → Q) → X → Y would recursively render in natural language naïvely as "Y whenever X and Q whenever P", even with some more sophisticated algorithm to remove the clunkiness, writing "Y whenever X and P → Q is just much clearer.

Mathematical expressions were pretty printed using Lean's pretty printing engine. However, the Lean 3 pretty printer needs a metavariable context in order to render, so it was necessary to add a tactic state object alongside the Act objects. It was necessary to store this context separately for each act because some metavariables would become solved through the course of the proof and cause confusing statements such as "by setting ε to be ε", where it should read "by setting η to be ε". Another printing issue was in the printing of values created through destructuring existential variables, which would be rendered as classical.some.

3.6.8. Summary

In this section, I detailed the workings of the natural language write-up component of the HumanProof system. I gave an overview of the standard architecture pipeline and then discussed the areas of novelty, namely the approach to producing suitable noun-phrase string from type-theoretical telescopes and on the verbalisations multi-apply steps.

3.7. Conclusion

In this chapter, I have introduced a new Box development calculus for human-like reasoning and demonstrated its compatibility (Section 3.4, Appendix A) with the development calculus of the Lean theorem prover. I have outlined the structure of a set of box-tactics within this calculus that allow for the creation of both formal and natural-language proofs of this output.

I then detailed the natural language generation component of HumanProof. The component can produce readable proofs of simple lemmas. Supporting larger projects is left for future work.

In the next chapter, we will discuss a new component to enhance the Box system for use with equational reasoning. I will make use of the work presented in this chapter in the evaluation (Chapter 6).

I will finish this chapter with some thoughts on future directions for the Box datastructure. A more general outlook on future work can be found in Section 7.2, where I also discuss potential future directions in applying deep learning to natural language generation.

3.7.1. Future work: 𝒪-critics

An avenue for future research is the definition of some additional box-tactics for the Box datastructure that allow it to work in a similar fashion to Ireland's proof critics [Ire92[Ire92]Ireland, AndrewThe use of planning critics in mechanizing inductive proofs (1992)International Conference on Logic for Programming Artificial Intelligence and Reasoninghttps://doi.org/10.1007/BFb0013060]. Recall from Section 2.6.2 that proof critics (broadly speaking) are a proof planning technique that can revise a proof plan in light of information gained from executing a failed plan. 𝒪-boxes can support a similar idea as I will now exemplify in (3.45), where the statement to prove is ∀ 𝑎 𝑏 : ℝ, ∃ 𝑥 : ℝ, (𝑎 ≤ 𝑥) ∧ (𝑏 ≤ 𝑥). The proof requires spotting the trichotomy property of real numbers: ∀ 𝑥 𝑦 : ℝ, 𝑥 ≤ 𝑦 ∨ 𝑦 < 𝑥, however it is difficult to see whether this will apply from the goal state.

At this point, one can spot that the lefthand Box is no longer possible to solve unless one assumes 𝑏 ≤ 𝑎. However, rather than deleting the left-hand box, we can instead use this information as in (3.46).

The remaining research question for putting (3.45) and (3.46) into practice is to determine some heuristics when it is appropriate to perform 𝒪-intro (step ②) and step ④, where an instance ℎ : 𝑏 ≤ 𝑎 ∨ ¬ 𝑏 ≤ 𝑎 is introduced. What is an appropriate trigger for suggesting the manoeuvre in ④,⑤,⑥ to the user?